- Цветы и растения
- Аквариум и рыбы
- Для работы
- Для сайта
- Для обучения
- Почтовые индексы Украины
- Всяко-разно
- Электронные библиотеки
- Реестры Украины
- Старинные книги о пивоварении
- Словарь старославянских слов
- Все романы Пелевина
- 50 книг для детей
- Стругацкие, сочинения в 33 томах
- Записи Леонардо да Винчи
- Биология поведения человека
Главная  Менеджмент Менеджмент  Конспекты лекций Конспекты лекций  Управління спецпроектами (конспект лекцій НУДПСУ) Управління спецпроектами (конспект лекцій НУДПСУ) |
Управління спецпроектами (конспект лекцій НУДПСУ)
Упорядкування сітьового графіка
Припустимо, що при складанні деякого проекту виділено 12 подій: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 і 24 роботи, що їх поєднують: (0, 1), (0, 2), (0, 3), (1, 2), (1, 4), (1, 5), (2, 3), (2, 5), (2, 7), (3, 6), (3, 7), (3, 10), (4, 8), (5, 8), (5, 7), (6, 10), (7, 6), (7, 8), (7, 9), (7, 10), (8, 9), (9, 11), (10, 9), (10, 11). Склали вихідний сітковий графік 1.
Упорядкування сітьового графіка полягає в такому розташуванні подій і робіт, при якому для будь-якої роботи попередня їй подія розташована левіше і має менший номер у порівнянні з завершальною цю роботу подією. Іншими словами, в упорядкованому сітьовому графіку всі роботи-стрілки розташовані зліва на право: від подій з меншими номерами до подій з великими номерами.
Розіб'ємо вихідний сітьовий графік на кілька вертикальних шарів (обводимо їх пунктирними лініями і позначаємо римськими цифрами).
Помістивши в І шарі початкову подію 0, думкою викреслимо з графіка цю подію і усі вихідні з неї роботи-стрілки. Тоді без вхідних стрілок залишиться подія 1, що утворює ІІ шар. Викресливши думкою подію 1 і усі вихідні з неї роботи, побачимо, що без вхідних стрілок залишаються події 4 і 2, що утворюють ІІІ шар. Продовжуючи цей процес, одержимо сітковий графік 2.
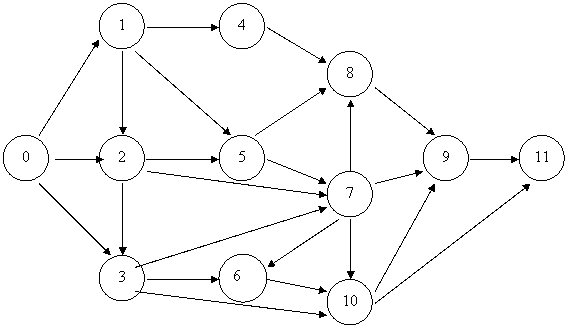
Рис.5.3. Неупорядкований сітьовий графік
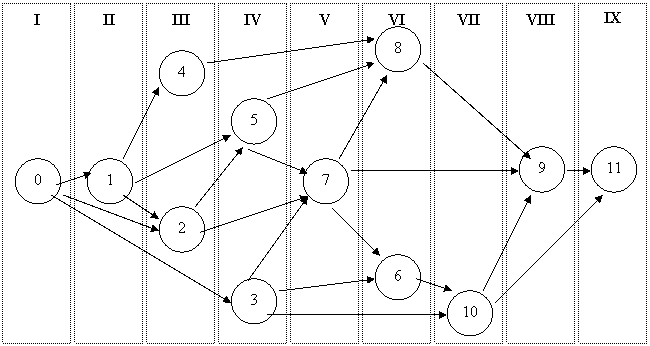
Рис.5.4. Упорядкування сітьового графіка
Тепер бачимо, що первісна нумерація подій не зовсім правильна: так, подія 6 лежить у VІ шарі і має номер, менший, чим подія 7 з попереднього шару. Те ж можна сказати про події 9 і 10.
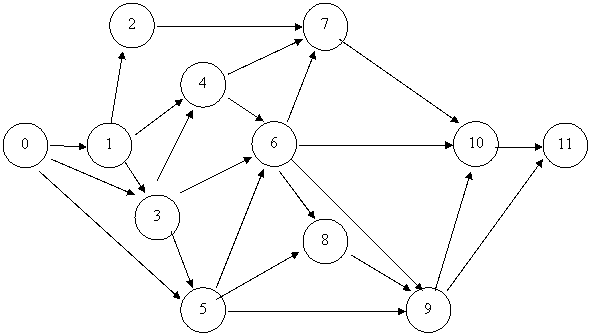
Рис. 5.5. Упорядкований сітьовий графік
Змінимо нумерацію подій відповідно до їх розташування на графіку й одержимо упорядкований сітьовий графік (рис.5.5.). Варто помітити, що нумерація подій, розташованих в одному вертикальному шарі, принципового значення не має, так що нумерація того самого сітьового графіка може бути неоднозначною.
Created/Updated: 25.05.2018