Secrets of view and science geometry

The visual system is a binocular (stereoscopic) optical system of a biological nature that evolved in animals and is able to perceive the electromagnetic radiation of the visible spectrum (light), creating a sense of the position of objects in space. The visual system provides a vision function.
Human vision (visual perception) is a process of psycho-physiological processing of images of objects of the surrounding world, carried out by the visual system, and allows one to obtain an idea of the magnitude, shape (perspective) and color of objects, their relative position and distance between them. According to various sources, from 80% to more than 90% of the information a person receives through vision.
Geometry (from other Greek lands and measure) is a branch of mathematics that studies spatial structures and relationships, as well as their generalizations.
We are used to trusting our eyes and we never ask ourselves why the same object looks bigger close, and in the distance is shallow? Or why do different objects sometimes appear to be the same size? The mechanisms of vision are very complex, but some of its features can already be explained on the basis of geometric representations.
What is the angle of view
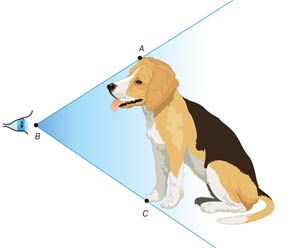
The angular size of an object is the angle of view under which the entire object is visible (in this case, the angle of the ABC).
Every object has linear dimensions: length, width and height. But as soon as it falls into our field of vision, it acquires one more dimension - a corner one. Let's see what that means. When we look at an object, through each of its points it is possible to draw from the eye a ray called the ray of sight. It is clear that there will be infinitely many of them. Any two lines of sight form a corner of view. The angle of view under which the object is seen entirely, and it is customary to call the angular dimension of the object. Like every flat angle, it is measured in degrees, minutes, seconds or in radians.
The concept of angular size is used in geometrical optics, geodesy, astronomy. It also occurs in geometry, but here it is customary to speak about the angle of view, under which the given segment is "visible" from this point-the height of the figure, its diameter, and so on.
The angular dimension depends on the choice of the observation point, which is easy to verify by measuring it from two points located at different distances from the object. Depending on the nature of the object, the amount of the angle of view under which it is visible is determined by means of special instruments, for example, a theodolite is used for measurements in the terrain, the sextant is used to determine the height of celestial objects above the horizon.

Measure the height of the luminary with the help of Yakov's staff.
In ancient times, more primitive tools were used for the same purpose. One of them is Yakov's staff, the predecessor of the modern sextant. It was a rod on which the cross-section rake slid; The bar was marked with fissions corresponding to certain angles (they were previously measured by a protractor). The observer brought one end of the staff to the eye, the other pointed toward the measured object and then moved the rack until it at one end "touched" the horizon line, and the other - the celestial object. After that, there was only "to take readings" - to see what division on the rod corresponds to the rake. This handy and simple tool is easy to make by yourself, it is quite suitable for approximate angles measurement in any plane.
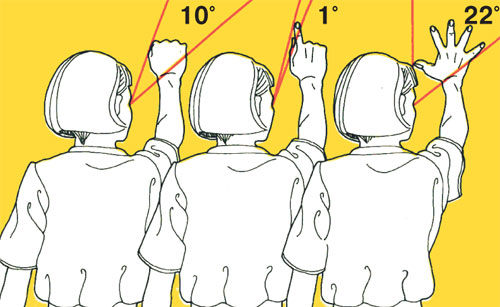
The hand is a natural protractor.
Finally, you can estimate the angular size of an object literally with "bare hands". A hand will serve as a protractor, if, of course, you know some corners. For example, the finger of the index finger of the arm stretched out in front of us is seen at an angle of approximately 1 degree, the fist at an angle of 10 degrees, and the gap between the ends of the placed thumb and little finger is at an angle of 22 degrees.
Angular size and distance
The angular size of an object is not constant and depends on the distance of the object from the eye: the further the object, the less the angle of vision under which it is visible.
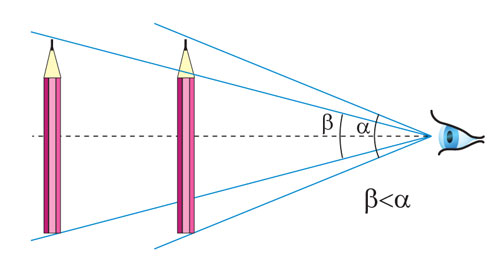
One and the same object can visually have different sizes depending on the distance from the eye of the observer.
To understand the cause of this phenomenon, we recall that on the retina of the eye the image of the object is obtained in reverse and reduced. When removing an object, its image on the retina becomes smaller, so it seems to us diminishing. When the distance is reduced, the image, on the contrary, increases and the object seems to increase. In the language of geometry, this means that the magnitude of the angle of view is inversely proportional to the distance to the object.
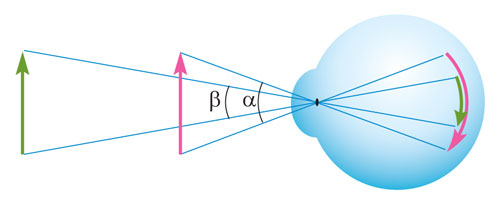
The image of the object on the retina is obtained by turning upside down (reverse) and decreasing.
This feature of sight helps to understand some of our actions and phenomena around us. Why, for example, to consider the details of a painting hanging on the wall or a small font on the page of a book, one has to approach the canvas closer or bring the text to the eyes. The answer is simple: we need to enlarge the image on the retina, and for this we need to increase the angle of view, which we do, reducing the distance to the object.
Another example. Imagine two parallel lines running parallel to the distance (railroad tracks, the edges of a straight-line highway). They seem "convergent" at one point. The same impression is created by rows of telegraph poles or trees along the road. Vision seems to try to convince us that, contrary to the laws of geometry, parallel lines intersect. But this is only an illusion that arises from the apparent decrease in the distance between the straight lines as they are removed.
From one angle
Often you have to deal with another situation. If we consider objects of the same shape, but of different linear dimensions under the same angle of view, then it seems that their dimensions are equal. This is confirmed by a simple experiment. Line up several matryoshkas by looking at them and look at them from the side of the smallest figure, and then slowly step back, without changing the direction of the look. You will see how the dolls begin to "merge", blocking one another. Finally, when you move a little distance, only one matryoshka will be visible - the one closest to you. If you now move the figures to the sides so that they are all completely visible, then visually the dolls will appear to be the same size.
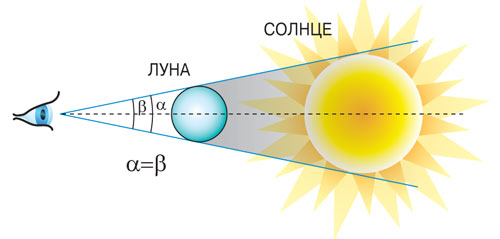
The geometry of a total solar eclipse.
A similar phenomenon can also be observed in nature. For example, with a total solar eclipse, the lunar disk accurately obscures the solar disk. At this moment, the observer from Earth sees both celestial bodies from one angle. It would be impossible to see such a unique phenomenon if the linear dimensions of the Sun and the Moon, and also the distances from them to the Earth, did not consist in a definite mathematical dependence.

From one angle, the apparent linear dimensions of objects seem to be the same.
From the point of view of geometry, in both cases we are dealing with the similarity of figures, more precisely, with homothety, with a center coinciding with the eye of the observer. Therefore, if two similarly shaped objects are visible under one angle of view, then their linear dimensions differ by the same factor, how many times the distances to objects differ. Thus, the diameters of the Sun and the Moon (D and d) and the distance from these bodies to the Earth (L and l) are related by a simple formula:
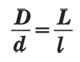
We did not reveal all the secrets of vision. Features of vision, when a person looks with two eyes, an explanation of some visual illusions, the creation of visual effects in architecture and painting.
Candidates of pedagogical sciences Marina YUGUPOVA and Natalia KARPUSHINA via nkj.ru


Comments
Commenting on, remember that the content and tone of your message can hurt the feelings of real people, show respect and tolerance to your interlocutors even if you do not share their opinion, your behavior in the conditions of freedom of expression and anonymity provided by the Internet, changes Not only virtual, but also the real world. All comments are hidden from the index, spam is controlled.