§ 7 Principles of adjusting and adjusting the induction counter

For a more complete understanding of the operation of the induction counter, let us consider the ways and basic principles of its adjustment:

Opposing and additional moments.

The torque generated by the resulting electromagnetic force will drive the disk. The frequency of rotation of the disk will be determined by the frequency of the network and the number of pairs of poles and will practically not depend on the load.
In order for this described induction system to be converted into a measuring instrument, it is necessary to create a counteracting torque that varies in proportion to the change in the measured quantity. Then to each value of the measured quantity there will be a counteracting moment at which equilibrium comes, that is, M _bp = M _against . Equilibrium can be static and dynamic. In all analogue electrical measuring instruments, the equilibrium of moments is static, that is, when measuring, the needle of the device deviates by some angle proportional to the measured value, and remains stationary. The counteracting moment for such devices is usually achieved by tightening the coil spring.
With dynamic equilibrium, the moving element of the measuring system, for example the disk of the induction counter, rotates at a uniform speed of rotation, and in this case the condition Mpp = M is maintained
The counteracting moment for the rotating disk is due to the inductive braking torque with the help of a permanent magnet M (see Fig. 1), encircling its poles with a disk. As the disk rotates, it crosses the magnetic flux Fm of a permanent magnet and induces an emf in it. E = c _{2 *} Ф _т* n , which creates a current i = e / r in the disk, where r is the resistance of a part of the disk in which the current is closed, bn is the number of revolutions of the disk per unit time.
Since the flux Φτ and the current in the disk are spatially shifted by an angle of 90, a force of mutual flow and current is created equal to Φm i , directed against the motion of the disk and creating a braking moment equal to:
M _vs = c _{1 *} Ф _{т *}i = c _{2 *} Ф _т²_* n = c _{3 *} n
Thus, the counteracting moment created when the disk is rotated by a permanent magnet is proportional to the rotational speed of the disk, and also depends on the radius of application of the braking force, i.e. From the position of the poles of the magnet from the center of rotation of the disk.
In addition to the main moments - the moments of rotation and the counteracting moment, a number of additional moments act on the counter disk, of which a part is parasitic, such as the friction moment, induction braking moments from the intersection of the workflow disk, from the skewing of the electromagnet cores, and one - created artificially for Compensation of friction.
The frictional moment is created by friction of the disc supports in the bearings, the counting mechanism and the disk about the air. This moment consists of a constant part and a variable that has a complex dependence on the rotational speed of the disk. When designing, measures are taken to reduce the frictional moment by using solid supports and special materials, an increased class of gears, etc., and also by creating a compensation torque.
The inductive braking torque resulting from the disc crossing of the operating circuit of the voltage circuit is practically constant (depends on the constancy of the applied voltage) and is added to the counteracting moment of the brake magnet. However, with increasing and decreasing stress, this moment, which depends on _u² = U ² , introduces some additional error into the measurement. The inductive braking torque of the series circuit is proportional to the square of the load current (since Ф2 ~ I2 ) and increases with the load, increasing the negative error of the counter. The moments from the skewing of the cores do not depend on the speed of the disk and are not separately considered.
The compensation torque is usually created by means of a steel screw located at the pole of the voltage circuit electromagnet parallel to the disk, as shown in Fig. 4.

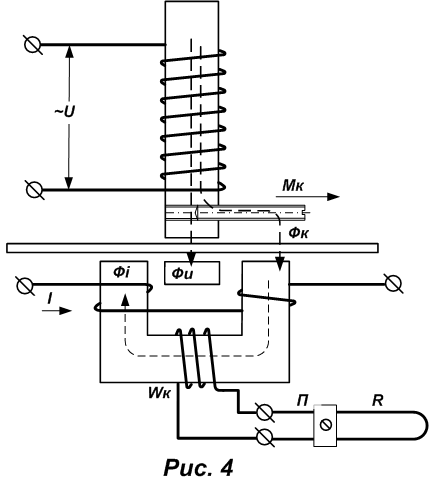
Fig. 4 Schematic diagram of regulation of the internal angle of the counter.

The currents induced in the rotating disk by the electromagnet of the voltage circuit interact with the magnetic flux of the steel screw branching off from the total flow, and create a small torque, the magnitude of which can be regulated by screwing and unscrewing the screw. The direction of the moment at the indicated position of the screw is positive, i.e. From the pole of Ф u to the extended end of the screw. If the screw is screwed in so that its end is protruded more from the opposite side of the pole, then the direction of the moment will change to the opposite. As can be easily verified, the compensation torque will be proportional to the square of the voltage.

So, draw conclusions from this paragraph:

1. To eliminate the so-called "self-propelled" counter, an adjusting screw is used, so sometimes, if it is possible to open the counter, it is possible to screw in the adjusting screw and the counter will slowly spin back when there is no load. But the method is too straightforward and easily detectable.

2. To adjust the internal angle of the counter, the adjustment resistance R is applied, that is, this resistance is responsible for the counter counting only the active energy . If the adjustment is knocked down, the counter will take into account reactive energy in addition to the active one. This is an important note for the ways of rewinding the counter called "Reactive Energy Generator". These methods will only work when the meter is adjusted down.