Start of section
Production, amateur
Radio amateurs
Aircraft model, rocket-model
Useful, entertaining 		Stealth Master
Electronics
Physics
Technologies
Inventions 		Secrets of the cosmos
Secrets of the Earth
Secrets of the Ocean
Tricks
Map of section
Start
Forum
Use of the site materials is allowed subject to the link (for websites - hyperlinks)

Navigation: =>

Home / Patent catalog / Catalog section / Back /

WIND POWER PLANTS. Wind turbines
INVENTION
Patent of the Russian Federation RU2101560

SCREW WINDER

SCREW WINDER

The name of the inventor: Smulsky II; Melnikov VP; Kavun I.N.
The name of the patent holder: Earth Cryosphere Institute SB RAS
Address for correspondence:
Date of commencement of the patent: 1996.04.09

Use: in wind power, namely in wind turbines, which convert wind energy into rotor rotation. SUMMARY OF THE INVENTION: The screw wind turbine comprises a shaft and screw blades mounted thereon. In order to increase the energy efficiency, the helical blades are funnel-shaped. The shape of the funnel-shaped helical surface is described by a monotonous function of radius, a particular case of which is an oblique line. In this case, the funnel-shaped surface is an oblique helicoid. For certain geometric parameters, the oblique helix unfolds into a plane. Then the funnel-shaped helical blade can be made of a flat annular preform. The wind turbine with funnel-shaped helical blades in an inclined position is more effective than a screw auger with straight helical blades. In addition, it can work in a vertical position and not depend on the direction of the wind. In comparison with other vertical wind turbines, it has a higher energy efficiency: a higher wind energy utilization factor than the Savonius wind turbine, and a higher energy production at low speeds than the Dar'i-like wind generators, and a less stressed construction and creates smaller acoustic, electromagnetic And environmental impacts.

DESCRIPTION OF THE INVENTION

The invention relates to wind power, namely to wind turbines, which convert wind energy into rotor rotation.

The Savonius windmill [1] is known, which contains a vertical shaft and blades installed along it, which are s-shaped in the normal section from the rotor axis. The torque arises from the different resistance of the convex and concave parts of the rotor. Savonius's windorower belongs to the class of slow-moving ones with a high speed of z 1 [2] Wind power factor of such a rotor is low: 0.1-0.15.

Daryer windmillers [2] and Darye-like rotors of the Hydroproject design [3] are known, which contain a vertical shaft connected to the shaft and longitudinally spaced narrow blades distant from it, the plane of which constitutes an acute angle with a plane tangential to the surface of the rotor. Along its length, the blades can be rectilinear (wind turbines of the "Hydroproject" or arc-shaped (wind-driven "Daria").

These rotors belong to the class of high-speed ones with a high speed of z 6, and the wind energy utilization factor reaches 0.3-0.35 [2] The disadvantage of these rotors is the high centrifugal load due to the high rotation speed. In these designs, large bending moments arise in the blades and knots of attachment of blades to the shaft. In addition, there is a change in the flow conditions of the blade during a single revolution, cyclically repeating millions of times. This causes fatigue phenomena and leads to the destruction of the rotor elements and serious accidents. The cyclic interaction of the blades with the air flow leads to the generation of acoustic oscillations, i.e. To aerodynamic noise, which prevents the use of wind turbines in populated areas. Cyclic operation creates a cyclic change in the electromagnetic characteristics of space (electrical and magnetic permeability), which leads to the modulation of electromagnetic waves and the violation of radio and television signals. All these disadvantages, except those caused by speed, are inherent in the Savonius rotor. In addition, Darye-like rotors, due to the high speed of the blades and the weak darkness of the contour of rotation, destroy birds that enter the rotor's rotation zone.

Known is a screw type wind turbine [4] adopted as a prototype, which contains a shaft and associated straight helical blades which, in the normal section to the axis of the rotor, have radial cross sections. The mathematical form of such helical surfaces is a direct helicoid and is described by a parametric system of equations [5]

The disadvantage of a screw rotor with straight helical blades is that it operates in an inclined position, therefore it requires a special supporting structure, and its efficiency depends on the direction of the wind, thereby reducing the efficiency of using wind energy. In addition, a straight helicoid is a surface of double curvature and does not unfold into a plane [6] Therefore, it must be made from a large number of flat sectors or subjected to stamping, which leads to an increase in the cost of the wind turbine.

The technical problem solved by the invention is to increase the efficiency of using wind energy, simplifying the design and manufacturing technology of the screw rotor.

To solve the technical problem in a screw rotor containing a shaft and screw blades fixed on it, the latter are made funnel-shaped with Cartesian coordinates of points on the surface



Where the z axis is directed along the axis of the wind;

R is the radius of the distance from the point to the axis of the wind;

V polar angle in the cross section of the wind turbine;

S pitch of the screw;

F (r) is a monotonically increasing function of the radius.

Funnel-shaped helical blades can be made in the form of oblique helicoid, which is described by formulas

F (r) = (rr 1 ) ctg ( ); = Arcsin ((r 2 -r 1 ) / h),

Where r 1 and r 2 are the inner and outer radii of the auger;

The angle between the axis and the forming oblique helicoid;

H Height of helical blade.

The height of the oblique helix blade is calculated by the formula



In this case, the funnel-shaped helical blade can be made of a flat ring with an inner radius



In addition, the auger windscreen can be installed vertically. In this case, its operation does not depend on the direction of the wind.

1 schematically shows a front view of a screw auger with funnel-shaped helical blades; FIG. 2 shows in two projections (front view and top view) the images of helicoids: a) straight; B) funnel-shaped; C) oblique. The length of the helicoid is equal to the pitch of the screw s.

The screw wind turbine is installed vertically and contains a shaft 1 and funnel-shaped screw blades 2 fixed to it (FIG. 1 shows a three-auger screw). The shaft 1 of the windmill is connected to the mast 3 via bearing bearings: the upper 4 and lower 5, in which the wind turbine is able to rotate. The mast 3 is mounted in the hinge 6 and secured with bracings 7. The rotation from the shaft 1 through the gear 8, the multiplier 9 is transmitted to the generator 10. In areas with the same wind direction, the windmill can be used in an inclined position 11.

In the direct helicoid (Figure 2, a), the generator 12 is directed along the radius. It is known [5] that it is described by formulas



Where x, y, z are the Cartesian coordinates of the points of the helical surface, the z-axis being directed along the rotor axis;

R is the radius of the distance from the point to the axis of the wind;

V polar angle in the cross section of the wind turbine;

S step screw.

SCREW WINDER

In the process of changing the angle v, the coordinate z according to formula (I) varies in proportion to v and is the same for all points of the generator, therefore all the generators in the resulting surface are horizontal. 2, a-c show the order of construction of helicoids. The frontal and horizontal projections are divided into the same number of parts. The odd small digits 1,3,5, (Fig. 2, a) show the projections of the point of the generatrix on the outer side of the helicoid, with even figures 2,4, points on the inner side of the helicoid. The areas of the surfaces in the front view are equal to the left and right of the axis and their curvature is the same. Therefore, with a horizontal wind, the torque to the left and right of the axis is the same and the rotor does not rotate. Thus, if the wind v is directed perpendicular to the axis of the rotor (a 90 o ), then due to the symmetrical arrangement of the blade parts on both sides of the rotor axis, the torque is balanced and the rotor does not rotate. If the angle between the axis of the rotor and the wind decreases (a <90 ), Then the parts of the blades on one side of the rotor axis are rotated to the wind by an edge, and on the other plane, as a result of which the torque from the second side exceeds the torque from the first and the rotor starts to rotate. At a certain angle a opt which depends on the length of the rotor L and step S, the torque reaches a maximum, and with a further decrease ( ---> 0), the torque is reduced to a certain value. In connection with this, such a screw rotor with helical blades having a straight helical profile (1) is used in an inclined position.

The funnel-like helical surface (Fig. 2b) is described by formulas



Where the z axis is directed along the axis of the rotor;

R is the radius of the distance from the point to the axis of the wind;

V polar angle in the cross section of the wind turbine;

S pitch of the screw;

F (r) is a monotonic function of radius.

2, b shows a funnel-shaped helicoid, where the generator 13 is a monotonous function of the radius z 0 = f (r), for example,

F (r) c (rr 1 ) n , (3)

Where c and n are any numbers, for example, c 0.1; 0.3; 1.5; N0.5; 1; 2;), r 1 is the radius of the inner boundary of the helicoid. In the process of changing the angle v, the coordinate z according to formula (2) is different for points of the generator 13 located at different radii. For example, on the inner radius of the funnel-shaped helicoid, the points of the generatrix are denoted by small digits 3, 6, 9. For the same generators, the midpoints 2, 5, 8 have larger z coordinates, and the z-coordinates at the outer points of the generators 1, 4, 7 are even larger. Thus, helical lines of the points of the helicoid at different radii are shifted along the z axis. Therefore, the helical surface becomes asymmetrical with respect to a plane perpendicular to the axis of the helicoid, i. E. Becomes funnel-shaped (Fig. 2b, frontal view). Due to the funnel shape, when the surface areas are equal to the left and right of the axis, their curvatures are not the same. With the right winding of the screw, as shown in FIG. 2, the surface on the left side is convex and the right side is generally concave. Therefore, the right side will interact more strongly with the wind flow, resulting in a torque that is directed to the right side. The wind turbine (Fig. 1, here the z axis is directed downwards) formed by the shaft 1 and several such funnel-shaped helicoids 2, on the one hand, will have concave surfaces from the axis, and on the other will be convex, due to which it will be rotated in the direction of the concave Surfaces. If the wind turbine is used in the inclined wind position 11 due to the funnel shape of the blades, its efficiency will be different: in the direction of the wind v (Figure 1), its efficiency is greater than in the opposite direction, and the efficiency in this direction exceeds the efficiency of the inclined screw rotor with straight helical blades.

In the particular case of the funnel-shaped helicoid (Fig. 2c), the generatrix is ​​an oblique line 14 that makes an angle with the helicoid axis. Such a helicoid is called oblique. It is further described by formulas

F (r) = (rr 1 ) ctg ( ); = Arcsin ((r 2 -r 1 ) / h),

Where r 1 and r 2 are the inner and outer radii of the screw rotor;

H Height of helical blade.

An oblique helicoid is a particular case of a funnel-shaped helicoid, for example, when describing it using formula (3), the oblique will be at c ctg ( ) And n = 1. In FIG. 2, at points 1, 3, 5 of the generator 14 on the outer radius of the helicoid are located above the points 2, 4, 6 on the inner radius. Therefore, like the helicoid in Fig. 2b, it has a funnel-like shape with concave surfaces to the right of the axis and convex to the left. In the general case, a straight line, a funnel-shaped and an oblique helicoid can not be unfolded into a plane [6]. However, there is one special case for an oblique helicoid, when possible. In this case, the height of the helical blade should be calculated by the formula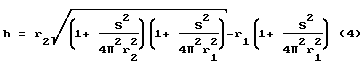



Then the helicoid blades can be made of a flat ring with an internal radius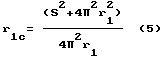



And outdoor

R 2c = r 1c + h. (6)

The inner surface of the ring with a radius r 1c will be joined to a shaft of radius r 1 along the inner helical line, since Expression (5) for the radius of the ring r 1c is known to be the radius of curvature of the helix's internal helix line. And the outer radius of the ring r 2c will form the outer surface of the helicoid of radius r 2 . For the purpose of checking, we calculate the lengths of the ring circles: inner l 1c and outer l 2c and helix lengths of the helicoid with a length equal to step s: inner l 1 and outer l 2 at parameters (4) - (6):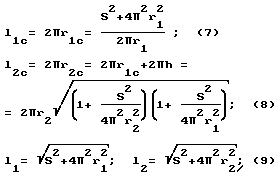



Now we determine how many times the circumference of the ring is longer than the length of the helix (inside k 1 and outside k 2 ):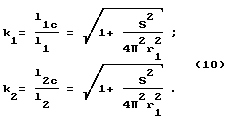



That is, k 1 = k 2 k. Because The radius r 2 is taken arbitrarily, then this result is valid for all radii of the helicoid. Thus, over all helical lines, the surface of an oblique helicoid with parameters (4) - (6) fits the same number of times in the ring circumference. As can be seen from the formula (10), from the ring with the parameters (4) - (6) it is possible to make a surface of a helicoid longer than one step. If necessary, you can collect a helicoid from the sectors of such a ring.

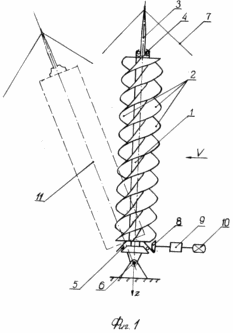SCREW WINDER

The screw auger (Fig. 1) operates as follows. With the direction of wind v, the load is perceived by the concave sections of the blades located to the left of the axis (Figure 3 shows a three-jawed funnel-shaped helicoid with right-handed guiding and a downward z-axis z), resulting in a left-handed torque. When changing the direction of the wind, the moment does not change. The wind turbine rotates in the bearing supports 4 and 5 and through the transmission 8 the rotation from it is transmitted to the multiplier 9 and then to the generator 10. The wind turbine can be mounted horizontally, connected below with the hinge 6, then with the help of stretches 7 and an additional post 1 is not shown) to be lifted to a vertical position by known methods. In areas with an unchanged wind direction, the windmill can be used in an inclined position so that the z axis forms an obtuse angle with the wind (in FIG. 1, position II). In this case, the funnel-shaped helical blades, as it were, grasp the wind flow. In an inclined position, a screw-type auger with funnel-shaped blades can also be used in orientable structures, as a screw rotor with straight blades is used, but its efficiency will be greater than that of a straight blade.

The sections of the screw blades of the screw rotor have an acute angle of attack with the incoming flow and the torque is created both by the difference in the resistance of the blades on both sides of the rotor and by the lifting forces. As a result, the wind energy utilization factor is increased in comparison with the Savonius rotor. In addition, during the revolution in the screw rotor there are no interruptions of the interaction of the blades with the wind flow in the direction of rotation, as a result of which the efficiency increases additionally to the values 0.3, as for multiblade windscreens [2]
The sections of the helical blade located under the wind load are supported by adjacent sections of the blades, so the stresses from the centrifugal and bending loads in the blades in the screw rotor are much smaller (by 1-2 orders of magnitude).

Within one revolution with the wind flow, practically the same amount of the surface area of ​​the helical blades interacts (only different parts of the blades vary). Therefore, in comparison with the Savonius and Darye rotors, the screw wind turbine with funnel-shaped screw surfaces is characterized by high smoothness of operation, absence of vibration and fatigue load caused by cyclic operation, significantly less acoustic and electromagnetic interference and reduced impact on birds and other animals (vibration for rodents and noise For terrestrial ones). The claimed wind turbine experiences smaller bending and centrifugal loads, especially compared to the Darrier winds and Darye-like rotors. In comparison with the Savonius rotor, it has a higher coefficient of wind energy utilization, and in comparison with high-speed Darje-like wind turbines, which have a small initial torque, the claimed wind turbine has a large energy sample at low speeds. Compared to a screw rotor with straight helical blades, the claimed wind turbine has a high efficiency in an inclined position, a simpler manufacturing technique (in the case of execution in accordance with formulas (4) - (6)) can be used in an upright position, which simplifies the wind installation constructively and allows It is more effective to use wind energy irrespective of its direction.

Several auger wind turbines with funnel-shaped helical blades having diameters D 2 and length L were made:

  • A three-wind windstorm with D 2 = 147 mm, L = 690 mm, according to the formulas (4) - (6);
  • A three-wind windrunner with D 2 = 200 mm, L = 920 mm, (the funnel-shaped helical surface was formed by five sectors one step);
  • A three-wind windstorm with D 2 = 184 mm, L = 920 mm, according to formulas (4) - (6);
  • A two-way wind turbine with D 2 = 200 mm, according to the formulas (4) - (6) (the helical surface is formed by three sectors by one step);
  • And other helicopters, including those with straight helical blades. These four rotors had a different funnel shape. All of them, under the influence of the wind flow, rotated well in an upright position. Especially effectively, the funnel-shaped helical wind turbines looked compared to inclined wind generators with straight helicoid blades with unstable wind direction. The funnel-shaped screw winds, despite the unstable wind, rotated almost uniformly, while for inclined non-orientable winds the rotation was changeable, and the inclined orientated winds constantly changed their position.

The wind turbines with straight helical blades and a wind turbine with funnel-shaped blades N1 were blown in a wind tunnel. As a result of purging it was found that in an inclined position the wind energy utilization factor x of the wind turbine N1 is 1.34 times greater than for a wind turbine with straight helical blades. Therefore, the claimed wind turbine has great energy efficiency both in vertical and inclined position.

INFORMATION SOURCES

1. Zubarev V.V. Minin V.A. Stepanov I.R. Use of wind energy in the North. L. Nauka, 1989, p. 208 (see p. 9).

2. Wind power. Ed. D. Renzo. Trans. V.Zubarev, M.O. Frankfurt, ed. Ya.I. Sheftera. -M. Energoatomizdat, 1982, p.272 (see page 44, figure 1.22).

3. Zubarev V.V. Mishin V.A. Stepanov I.R. The use of wind energy in the North. Science, 1989, p.208 (see page 32).

4. The patent of Russia 1225912.4 MKI F 03 D 5/00, 1986.

5. Mathematical Encyclopedic Dictionary.-M. Soviet Encyclopedia, 1988,848 p. (See item 141).

6. Gordon V.O. Sementsov-Ogievsky MA Course Descriptive Geometry. - M. Nauka, 1988, p.272 (see page 160).

CLAIM

1. A screw auger containing a shaft and screw blades fixed to it, characterized in that the helical blades are funnel-shaped with the Cartesian coordinates of the points of the surface



Where the Z axis is directed along the axis of the windmill;

R is the radius, the distance from the points to the axis of the rotor;

V is the polar angle in the cross section of the wind turbine;

S pitch of the screw;

F (r) is a monotone function of radius.

2. Wind turbine according to claim 1, characterized in that the funnel-shaped helical blades are made in the form of oblique helicoid and are described by formulas

F (r) = (rr 1 ) ctg ( );

= Arcsin ((r 2 -r 1 ) / h),

Where r 1 and r 2 are the inner and outer radii of the wind;

- the angle between the axis and the forming oblique helicoid;

H the height of the helical blade, calculated by formula

While the blade is made of a flat ring with an internal radius

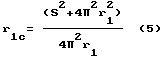
And the outer radius

R 2c r 1c + h.

3. Wind motor according to claims 1 and 2, characterized in that the wind turbine is installed vertically.

print version
Date of publication 17.03.2007gg