Start of section
Production, amateur
Radio amateurs
Aircraft model, rocket-model
Useful, entertaining 		Stealth Master
Electronics
Physics
Technologies
Inventions 		Secrets of the cosmos
Secrets of the Earth
Secrets of the Ocean
Tricks
Map of section
Start
Forum
Use of the site materials is allowed subject to the link (for websites - hyperlinks)

Navigation: =>

Home / Patent catalog / Catalog section / Back /

NON-TRADITIONAL DEVICES AND METHODS OF OBTAINING ELECTRIC ENERGY
INVENTION
Patent of the Russian Federation RU2165126

METHOD OF OBTAINING ELECTRICITY AND DEVICE FOR ITS IMPLEMENTATION

METHOD OF OBTAINING ELECTRICITY AND DEVICE FOR ITS IMPLEMENTATION

The name of the inventor: Prosekin AM
The name of the patent holder: Brown Leonid Borisovich; Bykov Nikolai Nikolaevich
Address for correspondence: 125206, Moscow, ul. Vuchetich 11, building 2, ap. 28, Prossekinu AM
Date of commencement of the patent: 2000.06.06

Use: to generate electricity in order to increase the efficiency of the process. SUMMARY OF THE INVENTION: Within a closed sealed vessel made of pumped-out and in the form of rigidly interconnected and coaxially located pipes of different diameters and lengths, a converter is used in a larger diameter pipe and shorter length, using as an MHD generator installed with a clearance relative to the walls of the cavity of the pipe , The electrodes of which are arranged in the longitudinal direction and with the possibility of forming a nozzle. The cavity of the vessel is filled with an alkali metal, which is used as sodium, and subsequent heating is carried out. The formation of an electric current generator on the electrodes of an MHD generator is obtained by the interaction of sodium with a gravitational field due to the simultaneous circulation of liquid sodium and sodium vapor in tubes of different diameters and lengths and passing the flow of vapor through the nozzle of the electrodes.

DESCRIPTION OF THE INVENTION

The invention relates to a method and construction of an apparatus for producing electric power.

A method for producing electric power is known, comprising forming a closed sealed vessel, placing a transducer inside it, including electrodes, current collectors, filling the cavity of the vessel with an alkali metal, and then heating the vessel to allow circulation of the alkali metal and for further formation of electric current on the electrodes while simultaneously feeding it To the load of the user.

Here, it is also known to provide an apparatus for generating electric power, comprising a converter arranged in the cavity of a closed sealed vessel filled with an alkali metal, adapted to be able to communicate with the load of the consumer and comprising electrodes, current collectors, and means for heating the vessel to allow circulation of the alkali metal (GB 1073326, cl. H 02 N 3/00, 21.06.1967 - analog and prototype).

A disadvantage of the known method and device for generating electricity is their low efficiency in use.

The technical result of this invention is to increase the efficiency in use by allowing the alkali metal to interact with a gravitational field.

This is achieved in the process in that sodium is used as the alkali metal, rigidly connected and co-located pipes of different diameters and lengths are used as a sealed vessel, a converter is used in a larger diameter pipe, using as an MHD generator installed with a clearance relatively The walls of the cavity of the tube, the electrodes of which are arranged in the longitudinal direction and with the possibility of forming a nozzle, the smaller section of which is directed towards the pipe of smaller diameter and longer length, before cleaning the interior of the cavity with an alkali metal, the inner walls are cleaned to allow their wettability by sodium, Vertical position with the placement of a smaller diameter pipe on top and preheating the vessel to a temperature of 150 ° C., filling the cavity of the vessel is carried out through the end of a pipe at the end of a pipe of a smaller diameter, preliminarily melted at 150 ° C. with sodium in an amount of 110-115 g, Vessel to a pressure of 10 -8 - 10 -10 mm Hg. Art. And sealing the through passage, and before the subsequent heating of the vessel, the latter is rotated through an angle of 180 ° to another vertical position for placing a larger diameter pipe on top, the subsequent heating of the vessel being carried out simultaneously with the supply of an electric current generator to the electromagnet; simultaneously heating the sodium to 800- 1300 ° C to allow circulation of liquid and formed sodium vapor and evaporation of sodium over the entire length of a tube of smaller diameter from the annular layer of liquid sodium, and the formation of an electric current generator on the electrodes of an MHD generator is obtained by the interaction of sodium with a gravitational field due to the simultaneous circulation of liquid sodium and steam Sodium in tubes of different diameters and lengths and passing the flow of steam through the nozzle of the electrodes, after the formation of electric current on the electrodes, the spent sodium vapor is condensed and the condensate drains from the larger diameter pipe into the smaller diameter tube to form a closed conversion cycle.

And in the device this is achieved by the fact that sodium is used as the alkali metal, the closed hermetic vessel is made of pumped-out and in the form of rigidly connected and co-axially located pipes of different diameters and lengths. In the tube of larger diameter and shorter length the converter is used, The MHD generator installed with a clearance relative to the walls of the tube whose electrodes are arranged in the longitudinal direction and with the possibility of forming a nozzle the smaller section of which is directed toward a pipe of smaller diameter and longer length, the means for heating the vessel is in the form of a spiral wound around The length of the surface of a pipe of smaller diameter, the power source of which is simultaneously connected to the magnet of the MHD generator.

It is advisable that the device has a process tube installed at the end of a pipe of a smaller diameter to fill the cavity of the tube with sodium through it, and the pipes and the process tube are made of steel, while in a pipe of smaller diameter the internal diameter is 24.0-35.0 mm, 1000-3000 mm, the wall thickness is 1.5-2.0 mm, in a larger diameter pipe the diameter is 150-200 mm, the length is 250-300 mm, the wall thickness is 1.5-2.0 mm, and the internal diameter of the technological The tube is 5.0-7.0 mm, the length is 50-100 mm, the wall thickness is 0.7-1.0 mm.

And it is expedient in the device to have brackets for fastening the protective casing of the MHD generator and the current collectors and current insulators located in them.

The essence of the invention is explained in the drawings, wherein:

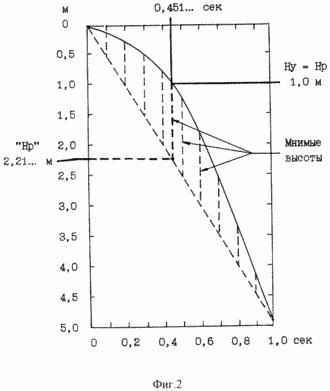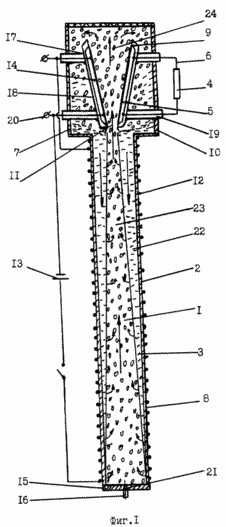
METHOD OF OBTAINING ELECTRICITY AND DEVICE FOR ITS IMPLEMENTATION

FIG. 1 shows an apparatus for generating electric power in an assembly.

FIG. 2 depicts the dependence of the height of the actual free fall of the liquid particles (solid parabola line) and the dependence of the uniform drop of the liquid particles (dashed line) on the time of fall in the gravitational field.

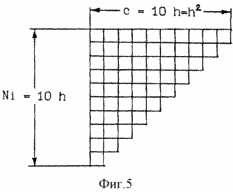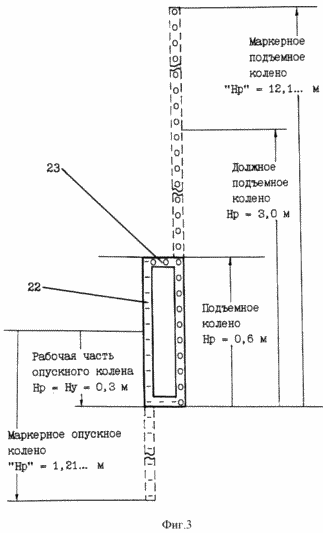
FIG. 3 - diagram of functioning of a closed pipe of an unbalanced communicating vessel.

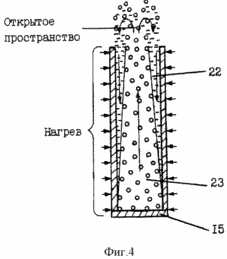
FIG. 4 - type of unbalanced vessel - open tunnel.

FIG. 5 is a diagram of the distribution of liquid particles.

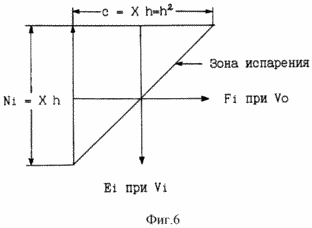
FIG. 6 is a diagram of the transverse transformation of energy-pulses.

FIG. 7 is a diagram of the length of energy packets and electromagnetic waves.

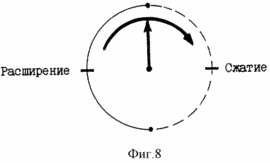
FIG. 8 is a diagram of the circle of the evolution of matter.

FIG. 9 - scheme of two-circle expansion-compression of matter.

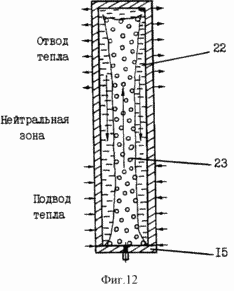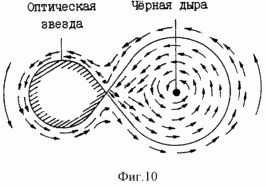
FIG. 10 is a diagram of the double star system of the Black Hole.

FIG. 11 is a four-phase space-time diagram.

FIG. 12 is a view of a heat pipe of gravitational action.

The electric power generating device comprises a closed sealed vessel 2 filled with alkali metal 3 located in the cavity 1, a transducer adapted to communicate with the load 4 of the consumer and comprising electrodes 5, current collectors 6 and means for heating the vessel 2 to allow the circulation of the alkali metal 3.

As the alkali metal 3, sodium was used.

The closed sealed vessel 2 is designed as a pumped-out and in the form of rigidly connected and co-axially arranged pipes 7, 8 of different diameters and lengths, a converter is used in the pipe 7 of larger diameter and shorter length, which uses an MHD generator 9 located with a gap with respect to the walls 10 Pipes 7 whose electrodes 5 are arranged in the longitudinal direction and allowing the nozzle to form, the smaller section 11 of which is directed towards the pipe 8 of a smaller diameter and longer length.

The means for heating the vessel 2 is in the form of a spiral 12 wound around the entire length of the surface of the tube 8 of smaller diameter, the supply source 13 of which is simultaneously connected to the magnet 14 of the MHD generator 9.

The device has a pipe 15 installed at the end 15 of a tube 8 of smaller diameter to fill the cavity 1 of the tube 8 with sodium 3 through it, and the tubes 7, 8 and the process tube 16 are made of steel.

In the tube 8 of smaller diameter, the inner diameter is 24.0-35.0 mm, the length is 1000-3000 mm, the wall thickness is 1.5-2.0 mm, in the pipe 7 of larger diameter the diameter is 150-200 mm, the length is 250- 300 mm, the wall thickness is 1.5-2.0 mm, and the internal diameter of the process tube 16 is 5.0-7.0 mm, the length is 50-100 mm, the wall thickness is 0.7-1.0 mm.

The device has brackets 17 for securing the protective casing 18 of the MHD generator 9 and the current collectors 6 and current insulators 19 located therein.

The device has terminals 20 for supplying direct current, a through channel 21 for filling the cavity 1 with molten sodium 3. Reference numeral 22 denotes liquid sodium, the reference 23 represents sodium vapor, and 24 represents a larger nozzle cross-section.

The device and method for generating electric power operates as follows.

Strictly connected with each other and coaxially located pipes 7, 8 of different diameters and lengths made of steel.

In the tube 7 of larger diameter and shorter length, the brackets 17 are mounted and the protective cylinder of the housing 18 with the electrodes 5 of the MHD generator 9 is fixed to them, and the current insulators 19 and current collectors 6 are placed inside the brackets 17.

The MHD generator 9 is placed with a gap in relation to the walls 10 of the cavity of the larger diameter pipe 7, and its electrodes 5 are disposed in the longitudinal direction so that a nozzle is formed, the smaller section 11 of which is directed towards the pipe 8 of a smaller diameter and longer length.

At the end 15 of a smaller diameter pipe 8, a through channel is formed and a steel process tube 16 is installed to fill the working body - sodium 3 therethrough.

Before filling the cavity 1 with an alkali metal 3, the inner walls of the tubes 7, 8 are cleaned to allow their wettability by sodium 3.

The formed sealed vessel 2 is set in a vertical position with the upper tube 8 of a smaller diameter placed on top and the vessel 2 is preheated by a spiral 12 wound around the entire length of the surface of the smaller diameter pipe 8, for example, 1000 W, to a temperature of 150 ° C.

The filling of the cavity 1 of the vessel 2 is carried out by pre-molten sodium at a temperature of 150 ° C. in an amount of 110-115 g.

The vessel 2 is then evacuated to a pressure of 10 -8 to 10 -10 mm Hg. Art. And sealing the through channel, in particular by brewing the process tube 16.

Prior to the subsequent heating of the vessel 2, the latter is rotated through an angle of 180 ° to another vertical position for placing a tube 7 of larger diameter on top.

Then, the vessel 2 is subsequently heated with simultaneous feeding of electric current generator 9 to electromagnet 14 MHD and at the same time sodium 3 is heated to a temperature of 800-1300 ° C to allow circulation of the formed liquid sodium and sodium vapor layers 22 and vaporization thereof along the entire length of the tube 8 of smaller diameter.

Moreover, an electric current is formed on the electrodes 5 of the MHD generator 9 by the interaction of sodium 3 with the gravitational field due to the simultaneous coordinated circulation of liquid sodium 22 and the sodium vapor 23 in tubes 7, 8 of different diameters and length and passing the vapor flow through the nozzle of the MHD generator 9.

The electric current from the current collectors 6 is supplied to the load 4 of the user, after which the spent sodium vapor is condensed and the condensate drains from the larger diameter pipe 7 into the smaller diameter pipe 8.

Below there is evidence of the possibility of obtaining electricity by using the claimed method and device by converting the kinetic energy of the flow of an electroconductive vapor of an alkali metal, in this case sodium, into a gravitational field, a liquid and formed sodium vapor.

A. Potential energy En and kinetic Ek are both functions of time. In the equation H = g · t 2/2, the time t reflects the extent of the fall space. In Fig. 2 shows the free fall heights H in a time t from 0 to 1 s (solid parabola line). The substitution in the equation E n M · g · H of the height H by H = g · t 2/2 allows us to characterize the transformation of E n into a finite value of E c in the time of fall in t seconds:

E n = E k = M · g 2 · t 2/2 = J / t s (1)

With the acceleration due to the gravity gravity g = 9.80665 m / s 2 and the altitude H = 1 m, the accelerated fall time t = 0.451 ... s, but the final velocity V of the accelerated (y) drop Vy = g · t = 4, 42 ... m / 1 s corresponds with 1 s. In this case, in the imaginary uniform (p) coordinates, the fall velocity Vp is 2 times less than the velocity Vy in the accelerated frame:

Vp = Vy / 2 = g · t / 2 = 2.21 ... m / 1 s (2)

Hence, the time t = 0.451 ... s in the first degree reflects a uniform fall in 1 s at pseudo-altitude "Hp" = 2.21 ... m (dotted line). In the equation, H = g · t 2/2, the time t 2 reflects a uniformly accelerated fall in height H = 1 m. The height of 1 m is the real part of the imaginary height "Hp", and with the velocity Vp = 1 m / 0.451. . . S = 2.21 ... m / 1 s, the uniform fall of the imaginary part of the altitude would continue "Hp = 2.21 ... m:

H / t = "Hp" = Vp = 2.21 ... m / 1 s (3)

Accordingly, for a uniformly accelerated fall in the mass M = 1 kg in height H = 1 m in time t = 0.451 ... s according to the equation (1) E n = E k = 9.80 ... J / 0.451. .. c, and the replacement of time t 2 by time t in the first degree in equation (1) with time t makes it possible to relate the energy E n = E k from 1 s to the imaginary uniform fall in pseudo-altitude "Hp" = 2.21 ... m:

E n = E k = M · g 2 · t / 2 = 21.7 ... J / 1 s (4)

For 1 s in the square, the real height of the accelerated fall of Hv or the slowed (h) rise of H3 is:

Hy, s = g · t 2/2 = g · 1 2/2 = g / 2 (5)

The quantity g / 2 is the conjugating height of a free fall or a 1-second rise in a square. Hence, the pseudo-altitude "Hp" of a uniform fall or rise in 1 s in the first degree is equal to . The value g / 2 conjugates the real heights Hy, s with imaginary heights "Hy, s":

"Hy, s" = Hy, s · g / 2) = Hy, s · g / 2 (6)

For example, at Hv = Hp = 0.3 m, the time t = 0.247 ... s. According to equation (6), the height "Hу" = 1,47 ... m. From the equation "Hу" = · "t" 2/2 (analog H = g · t 2/2) imaginary time "t" = 0.547. .. c, a "t" 2 = 0.3 s. Hence, the time t 2 = 0.0611 ... s reflects the drop height, and the time "t" 2 = 0.3 s not only reflects but also in numerical terms the height Hp = Hy:

Hp = Hу = "t" 2 = 0.3 m = "с" 2 (7)

When the triple conjugation Hp, Hv, s and "t" 2 at any moment of uniformly accelerated fall or evenly-delayed ascent, the imaginary time "t" 2 is equal to the real altitude Hp = Hy, h. Metric "Hp", "Hу, з" and "t" 2 are markers of conjugation of different frames of reference. In the marker space-time, the uniform heights "Hp" reflect the first degree of the pseudo-space of the fall or rise, and the accelerated and decelerated heights "Hу, з" - the square of the pseudo-space of the fall or rise:



B. We take the height H = 1 m. In the accelerated coordinates of the reference, the time of free fall t = 0.451 ... s or height H = 1 m can be divided into any number (N) of local intervals (i) of time (t) and space (h ) Fractional fall.

When the time t is divided by the number Ni = 100 t, the time t = t / Ni = 0.00451 ... s, and the height h = g · t 2/2 = 0.0001 m. For the height H, the number Ni = 10000h - This is the square of the number Ni = 100 m for the time t. In view of the difference in the square of the number of intervals h = 10000 and m = 100, the point mass M can not be localized at a single spatio-temporal level of incidence.

If we divide the mass M by 100 mass m, then their independent fall is also impossible, because each mass m must instantaneously fall at level 1 and at 100 levels h. In view of Ni = 10000h, each particle m should be virtually stretched in the range of 100 compressed levels h.

Spatio-temporal localization is achieved by dividing the height H. At Ni = 100h, the height h = 0.01 m, and the time of accelerated fall in height h is equal to S, which corresponds to equation Hence, the cycle of consecutive falling of a point mass M over 100 levels h leads to an extension of the initial time of continuous free fall t = 0.451. . . With in - up to 4,51 ... with. This time is composed of a cycle of 100 time periods and an accelerated fall in height H = 1 m. The cycle 100 of periods t will be denoted by the time T of discrete incidence:



Deceleration time from t to Eliminates the "square of the discrepancy" of the spatial and temporal localization of the point mass M under a fractional fall. With an equal number of space-time levels, the division of the mass M = 1 kg per 100 mass m makes it possible to carry out the batch transfer of E n to Ek with the distribution of the block 100 mass m along the height of the energy packet H = 1 m by 1 mass m at level 1 h. Proceeding from equation (4), at a momentary batch drop of the block 100 masses m in time t in its levels h is true:

The packet E n = E k = Ni · m · g 2 · t / 2 = 2.17 ... J / 1 s (10)

In terms of quantization, the energy packet is a discrete energy spectrum of the potential energy E n = 9.80665 J in the height H = 1 m. For the number Ni = 100, according to Eq. (10), the packet transfer of En into Ek in Less than the equation (4). This is explained by an excess of 10 times the time T = 4.51. . . From the cycle of discrete incidence of each mass m over time t = 0.451 ... with a continuous drop in the point mass M in height H = 1 m, i.e. Deceleration of the pumping time E n in Eк during packet dropping.

Since in equation (10) Ni · m = M, and Then the release of discrete portions of Eh in a packet drop can be calculated from the equation:

Package

C. The feature of accelerated fall is the cyclicity with the release of kinetic energy. In free fall, the rate increases from zero to the final value at the time of the fall. Only at this moment it is possible to allocate a portion of Eq. The release of Ek at a real uniform drop requires the continuous extraction of Ek directly during the fall, while simultaneous transfer of En into Ek. This condition characterizes the uniform fall as a uniformly conditioned motion, and the imaginary accelerated fall coordinates associated with it acquire the value of hidden variables.

The real uniform drop is the drop in the liquid in the pipe, which is realized due to the redistribution of 1/2 Ek from the lower half of the liquid column to its upper half. The liquid particles pass 1/2 of the pipe in a time equal to an accelerated fall from 1/2 the height of the pipe.

According to these known conclusions, in the tube, the liquid falls over 2 levels of Ni, For example, at a tube height of 0.6 m, the time t of free fall relative to the whole pipe is 0.329. .. from. According to formula (9), the discrete dip time along the pipe height is , And the time t = T / Ni = 0.247 ... s equals the latent accelerated fall time with 1/2 the pipe height. Hence, for the tube in equation (2), the velocity Vp is already the real fall function, and Vy is the imaginary drop function.

In Fig. 3 shows a closed pipe of an unbalanced communicating vessel with a knee height of 0.6 m. In the descending bend there is liquid, and in the lifting - the vapor of this liquid.

The liquid falls in 2 levels of Ni. At the upper level, 1/2 EK is borrowed continuously from the lower level, which makes it possible to realize a uniform drop in the liquid by eliminating the upper level from any other energy transformations. Therefore, only the lower 1/2 of the pipe is the working level of Ni, which participates in other transformations of En and Ek.

We take the difference in the densities of the liquid (L) and vapor (S) in 10/1 and compare the circulation in the vessel with the accelerated fall and slow rise in the free space of point bodies L = 1 kg and S = 0.1 kg. With the free fall of L along the working height, H y = ​​0.3 m, the time t = 0.247 ... s. According to the formula Vy = g · t, the finite velocity L is equal to 2,42. .. m / s. Passing the momentum of the pair, S will start a slow rise at a speed of 24.2 ... m / s and in time = 2,47 ... s will reach the height of Hz = 30 m.

According to the formula (4), the growth of Ek during the fall time t = 0.247 ... from the mass L = 1 kg is equal to the decrease in Eq during the rise time = 2,47 ... with the mass S = 0,1 kg. But at the same time the continuity of the "flow" of the mass (1 kg, 0.1 kg) and the bypass time (drop of 0.247 ... s, rise of 2.47 ... s) are "violated". Eliminating one of these "violations" will change the balance of the work of the detour.

According to the formula (6), the imaginary height of the accelerated fall is "H" = 1.478 ... m, and the slowed rise of "H3" = 147.8 m. Hence, according to equation (8), the imaginary descending pseudocolumn "Hp" of the marker balanced vessel is 1, 21 ... m, and the lifting leg "Hp" - 12.1 ... m. According to the formula (3), the imaginary marker bends "Hp" are equal to the real uniform velocities of the fluid drop Vp = 1,21 ... m / 1 s And the steam rise Vp = 12.1 ... m / 1 s.

In an unbalanced vessel the height of the working part of the dropping knee is 0.3 m, the mass of the liquid is 1 kg evenly falling behind 0.247 ... s. The weight of steam 0.1 kg in height 0.3 m is uniformly raised in the hoisting knee for 0.0247 ... s, and for 0.247. . . With the mass of rising steam is also 1 kg, i.e. In the vessel, the continuity of the mass flow of liquid and vapor is not disturbed.

But the mass flow moves at a difference of 10 times the time t = 0.247 ... with the fall of the liquid particles along the working height of 0.3 m and the time \ = 0.0247 ... with the rise of the vapor particles at an altitude of 0.3 m. With the height of the lifting knee 0.6 m, the particles of the vapor actually rise in the vessel in time = 0.0494 ... s.

Regarding the height of 0.3 m of the working part of the dropping knee with liquid, the vapor column tends to create a proper balanced vessel with a lifting leg of 3 m. However, this is impossible in an unbalanced vessel. In it, the steam rise is interrupted, unrealized above the pipe height of 0.6 m and the rise time = 0.0494. from. The working height of the lowering knee of 0.3 m is also the real part of the descending knee of a marker balanced vessel with a pseudostight "Hp" = 1.21 ... m.

It is the working height of 0.3 m of the descending knee that "forms" the proper and marker balanced vessel, and also predetermines the work of circumvention in a closed vessel in a real uniform, latent accelerated and marker reference system.

For a two-phase mass flow, M = 1 kg / 0.247 ... s according to formula (4), for a time t = 0.247 ... with a drop in liquid particles over an altitude of 0.3 m, the energy growth Et = 11.8. .. J / 1 s, and in time = 0,0494 ... with the rise of par- ticles in the altitude of 0.6 m, the energy loss E = 2.37 ... J / 1 s. The released energy (f) of the bypass operation is equal to Ef = Et - E = 9.51 ... J / 1 s.

Loss of E , Equal to 1/5 of the height of Et, reflects the difference in height of the lifting knees of an unbalanced vessel of 0.6 m and a proper balanced vessel of 3 m (work efficiency 0.8). With a liquid / vapor density ratio of 100/1, the asymmetry of knee heights is 1 to 50, and the efficiency is 0.98. At densities of 1000/1, the asymmetry of the knees is 1 to 500, and the efficiency is 0.998. And so on.

Hence, A. Einstein was right when he wrote back in 1936: "There is no doubt that in quantum mechanics there is a significant element of truth and that it will become a touchstone for any future theoretical framework from which ... it will be derived as a private Case "(5, p. 313).

D. Packet (quantum) pumping of En into Ek can be realized by tunneling, for example, in an open tunnel, which is a specific unbalanced vessel. In it, the knee of the steam is inside the liquid knee (Figure 4). The bottom of the tunnel is closed. Throughout the height of the vessel, the falling liquid evaporates and forms a vapor column. Steam rises, goes into open space and condenses there. The condensate returns to the top of the annular liquid column.

Tunneling with a uniform drop in a packet of liquid particles can be done by distributing them along a triangle of the mass wedge in Fig. 5. With the number Ni = 10h, the vertical cathete is equal to the height of 10 particles of the liquid. The horizontal leg is equal to the cross section of 10 particles of the ring column of liquid at the top of the tunnel. Hypotenuse is the zone of liquid particles boiling out. When the wedge particles fall at each level h, one particle of the liquid must be simultaneously boiled away, which requires matching the spatial parameters of the mass wedge.

Since the real uniform functions correspond to latent accelerated functions and the uniform decay is related to the time count in the first degree, and the accelerated one from the second, the matching of the real uniform coordinates of the wedge fall with its hidden accelerated fall coordinates requires the construction of all parameters of the mass wedge into a square.

We take the volume of 1 particle of liquid per cube with an edge h = 1 unit and area of ​​1 face equal to h 2 = 1 2 = 1 unit h. Hence, the area of ​​10 faces of the upper wedge leg, equal to 10 h, reflects the uniform quadrature of the small circle (c) of the upper level of the liquid column of the mass wedge: c = 10 faces h, with diameter Edges h. The quadrature of a small circle c = 10 faces has a latent accelerated quadrature of a small circle "c" = 10 faces 2 . For c = "c", they must be square-conjugated (see below) with large quadratures of circles.

In the uniformly accelerated circles (first-second degree), the quadrature of the large circle is C = c 2 = 100h = h 2 , and the square of the diameter d · d = 12.73 ... h = (h 2 ) equals the diameter "D" = 12.73 ... h of the latent accelerated large circle "Cу" = 127,3 ... h 2 .

The ratio "Cу" / C = 4 / Is the only coupling coefficient q = 1,273 ..., at which the diameter D = 1,273 ... cm is equal to the area of ​​the circle S = 1,273. . . See Factor q manifests itself multiple to the numbers 1, 10, 100, 1000, .... Hence, for q in the first degree, the smallest number of levels in the packet is Ni = 10, and q 2 predetermines the smallest number of uniformly-accelerated conjugate levels Ni = 100. Accordingly, the coefficient q coordinates quadratures of 4 circles (2 small and 2 large) real and hidden sections A liquid column at the upper level of the mass wedge. In this case, 1.0 unit of the real quadrature of the section is conjugate with 1,273 ... the unit of the hidden quadrature of the section.

According to formula (9), the spatial and temporal levels of the wedge are consistent by extracting the root from Ni = 100h = h 2 , whose Ni number is associated with q. In this way, in units of measurement h, the number of Ni in the wedge is mated to a large circle C through its diameter D by means of expression And at a known height of 1 level h in cm, the real value of D is:



The coefficient q matches the wedge with any number of Ni. For example, for arbitrary values ​​of H = 92 cm and Ni = 156, the height h = 0.589 ... cm. According to equation (12), D = 8.31 ... cm, with a radius R = 4.51 ... cm and area Circle S = 54.2 ... cm 2 . Calculation of the upper-level cross-section according to the usual formula S = (H / Ni) 2 · Ni coincides with the calculation of S by Eq. (12). The volume H · S in cm 3 corresponds to a column of liquid with a uniform section S over the entire height H. The actual volume of the liquid column is equal to 1/2 of this volume due to the decrease in the section S of the liquid to zero at the bottom of the mass wedge (the area of ​​the triangle is 1/2 From the square).

D. The uniformly accelerated time intervals for the falling of m particles of the liquid m correspond to the pumping of E n into E k, which can be expressed by discrete mean forces f by means of hidden fractional momenta (i) of the forces fi, as the action of f in time t, since m is the same in uniform and accelerated The coordinates of the fall on level 1 h.

Proceeding from the force f = m · g and the momentum of the force fi = f · m, the force pulse in the 1 drop interval h is equal to fi = m · g · m, where g · m = Vy. In the latent frame of reference, with the initial zero velocity v0 and the final accelerated velocity Vy, the increment in the amount of motion in time t is equal to the force impulse fi = m · V0 + m · Vy = m · Vy = m · g · t. Since in equation (6) the quantity g / 2 matches the height of Hy with the marker height "Hp", it also coordinates the height hy with "hp". Hence, the momenta of the force fi · (g / 2) = m · g · m · (g / 2) = m · g 2 · m / 2 at the fractional levels h can be expressed by the action of the momentum packet of forces Fi. Since the time t is expressed in the first degree in fi = m · g 2 · m / 2, the action of the pack of hidden impulses of the forces Fi of the mass block m is related to 1 s:

The package Fi = Ni · m · g 2 · m / 2 = Fi / 1 s (13)

Equations (13) and (10) are equivalent. They can be combined and, relying on equation (11), for the purpose of a unified expression of the energy and impulse equations, expressed by the hidden action of the energy-momentum packet (Ei):

Package

The fractional portions of the Ei packet are realized in the tunnel in a peculiar way. The falling particles of the mass wedge wedge between the inner surface of the tunnel and the vapor column inside the annular column of liquid. The horizontal vapor layers and liquid rings around them are located at an angle of 90 ° to the gravity vector. Therefore, only at an angle of 90 ° to the vapor column and to the wall of the tunnel tube, particles of the mass wedge can transmit the energy-momentum packet to the vapor particles.

The transformation of the vertical batch transfer of E n into E k into the horizontal action vectors of the mass wedge particles is a transverse quantization along the mass wedge cross (Fig. 5). In the cross along the vertical, there is a discrete process of escalating Ei with particles of liquid at a rate Vi, due to the number of Ni. Simultaneously, along the transverse component of the cross with the zero horizontal velocity of the fluid V0, impulses of the forces Fi on the fractional horizontal lines of the liquid-vapor particles are realized.

As a result, the vertical vectors of the action of the hidden portions of the package At a fractional-velocity drop in the fluid Are transformed along the cross into transverse discrete (with a width h) of the action vector of the hidden impulses of the packet forces At zero transverse velocity of fluid motion

E. At the smallest number of Ni = 100h uniformly accelerated discrete (d) levels of incidence, the upper level of the mass wedge contains 100 fluid particles. According to the arithmetic progression (1 + 100) · 100/2, the number of particles of the wedge is 5050. Hence, at the specific levels of the wedge, the average number of fluid particles (discretion) is d = 5050 / Ni = 50.50, and boils out 1 particle of liquid. When the wedge particles fall with a mass Mc = 1 kg, the mass of the wedge interacts in the tunnel with the mass of the boiled liquid Mb = Mc / d = 0.0198 ... kg.

Based on the masses of Mc and Mb, we compare the tunnel effect in the micro- and macrocosm. In the microcosm, in the potential well arising in the field of attractive forces, the penetration by the particles of the potential barrier during tunneling is related to the uncertainty relation. Macro-tunneling in the field of gravity, with the escape of particles from the tunnel, can be explained by classical physics.

The microcosm is described by the square of the probability amplitude. Therefore, in equation (14), the number Ni = 100 should be expressed without root extraction. At H = 1 m, the mass of the wedge Mc = 1 kg and the time of fall t = 0.451 ... s, Ei = Eк = 0.217 ... J / s. Hence, from the formula Ek = Mc · V2 / 2, the velocity of a uniform drop in the fluid is V = 0.659 ... m / s, and the time of fall along the height H = 1 m equals H / V = ​​1.51 ... s. According to formula (14), without extracting the root from Ni, at t = 1.51 ... s and Mc = 1 kg, the quantity Ei = Eк is 0.7296 ... J / s. This is the abstract packet energy (Ea), because it is calculated again after applying the equation Ek = Mc · V2 / 2, in which the velocity V does not reflect the packet value Ei = Ek according to equation (14).

Without extracting the root from Ni in the formula (14), the wedge transfers the energy Eb = Ei = 0.217 ... J / s to the boiled liquid Mb. With a mass of liquid Mb = 0.0198 ... kg, from the equation Eb = Mb · Vb 2/2, the velocity of the boiling liquid is Vb = 4.68. . . M / s. Since the discretion d reflects the mass ratio of the wedge and the mass of the boiled liquid, then with respect to the speed Vb, the velocity of the drop of the wedge fluid is Vc = Vb / d = 0.09273 ... m / s.

The values ​​of Ea, Vc and d are commensurate with the fine structure constant (0.007297 ..), the Bohr magneton (9.273 · 10 -24 J · ml -1 ), and the nuclear magneton (5,050 · ​​10 -27 J · ml -1 ), That is, the tunneling during acceleration of gravity on Earth 9,80665 m / s 2 reflects the interconnection and physical essence of these world constants.

The abstract energy packet Ea = 0.7296 ... J / s corresponds to the dimensionless value of the fine structure constant.

Since 1 J reflects the transport of matter by 1 m, when the matter is transferred by 1 cm, the energy Ea = 0.007296 ... sJ / 1 s is numerically equivalent to the fine structure constant. Hence, 1 cm and 1 s are the dimensions of the world constant, and the real "fine structure" of the energy splitting at Ni = 100 and H = 1 cm according to Eq. (14) is Ei = 0.0217153 ... sJ / s.

G. Interaction of particles of the microworld at an angle of 90 o corresponds to the transformation of Ei in the tunnel along the cross of the wedge of mass.

Quantization and tunneling reflect the originality of the nature of the microworld. It follows from the Schrodinger equation that if a particle is in a potential well, then "its energy assumes only certain special values ​​forming a discrete energy spectrum" (7, vol. 9, p. 102).

In a gravitational macrotunnel, too, a discrete energy spectrum (energy packet) is formed. Both the quantum Schrodinger equation and classical tunneling reflect how quantization in the form of a packet of discrete energy levels in an atom or in a gravitational tunnel arises from continuous functions of spatial variables.

Until now, the essence of the square of the probability amplitude has not been revealed. "What mechanism is hiding behind this law? ... Nobody could find any mechanism ... Physics ... gave up. \ R \ n \ r \ n We do not know how to predict what would have to happen in the given circumstances, but we are sure that it is unthinkable. We have to admit that we have changed our previous ideals of understanding nature, maybe it's a step back, but no one taught us how to avoid it! ... At present we have to limit ourselves to calculating probabilities. "We are saying" at the present time, "but we Very seriously we suspect that all this is for good already and to crack this nut to the person is too tough for the nature of things "(7, volume 3, p. 214).

However, "There are physicists who intuitively feel that our world can be described in some other way, that these uncertainties in the behavior of particles can be eliminated." They continue to work on this problem, but so far none of them has achieved any Substantial result "(7, volume 1, page 120).

The hidden variables of the particle wedge particle function are an analog of the square of the wave function in the Schrodinger equation, according to which "The wave function of an individual particle is ... a function of position, but generally speaking, it has no classical meaning" (7, vol. 9, p. 226).

The localization of individual particles in the tunnel is of classical importance, since the excess of the square of the Ni number of spatial levels over the number of Ni time intervals is eliminated due to the slowing down of the packet drop time of individual particles along the tunnel height.

Quantization and relativism are contradictory. "Strange as it may seem, it turns out (for reasons we have not yet figured out) that the combination of relativism and quantum mechanics seems to prohibit the creation of equations free of contradictions." Note: not because of the discrepancy with experiment, but from Internal contradictions "(7, volume 5, page 254).

The slowing down of the time of falling of the liquid particles in the tunnel can be considered a manifestation of relativism. Batch tunneling eliminates the contradiction between quantization and relativism, because it is the quantization that predetermines relativism. But the slowing down of the time for the fall of the liquid particles is a pseudorelativism, because The rate of time itself does not slow down.

Consequently, as applied to gravitational tunneling, quantum mechanics is a very peculiar, but still a private section of classical mechanics. Apparently, the classical principles of gravitational quantization are unified in micro-, macro- and megamore.

I. "There is a physical problem that is common to many sciences, very old yet, but still unresolved ... It's a long time ago, over a hundred years ago, left aside by science." No physicist could yet mathematically impeccably analyze It is an analysis of circulation or a vortex liquid.If you follow the evolution of a star, sooner or later we will come to the point where convection begins in the star, and from that moment on we do not know what will happen next "(7, vol. 1, p. 69).

Convection on the Sun can be carried out in tunnels, the presence of which indirectly confirms the granulation structure of its surface. "Granules are bright spots of more or less round shape, visible on the surface of the sun ... The size of granules is 150-300 km, the lifetime is 5-10 minutes. The granules are brighter than the intergranular intervals by 20-30%, which corresponds to the temperature difference on the average of 300 K. Granulation is the same at all heliographic latitudes Observations have shown the existence of cells in which the motion occurs in the horizontal direction from the center of the cell to its boundaries.The supergranules at the boundaries of the supergranules are strengthened.It is assumed that the supergranules reflect the existence at a depth of several thousand km below the surface of convective Cells of the same size "(1, vol. 24, p. 152).

Proceeding from these observations, the granules are the upper ends of open megatunnels, and the cells in the depth of the convective zone (0.2 radius of the Sun) are the lower parts of the tunnels. The role of tunnel tubes is performed by a magnetic field. In the climbing knee, the heated substance rises upwards, emerges from the tunnels, cools as it moves from the center to the boundary of the granules, then descends to the top of the rings of the diplegs and falls downward along the inner side of the magnetic shell of the megatunnels.

The granules reflect the presence of a cellular network of tunnels in the volume of the Sun's sphere, which taper towards its center. In the transverse transformation of Ei in megatunnels, the vector of action of the impulses of forces They are directed inside the circles from the rings of the incident substance towards each other in a plane perpendicular to the gravity vector, but not at an angle of 90 ° to the tapering shells of the tunnels. On the Sun "wherever you throw, everywhere the wedge" and when the ring vectors are decomposed Their "counter-transverse" action vectors press conical tunnels into the center of the Sun, thus preventing its destruction.

In the case of a conditioned working fluid, the liquid-vapor pressure will not occur when the liquid evaporates from the lateral generatrix of the cone, since the vapor particles leave the liquid at an angle of 90 ° to its surface, and not to the force vector of gravity. For this reason, the counter-transverse effect of the impulses of forces will disappear And, accordingly, the effect of indentation. Without evaporation from the lateral generatrix, the liquid column has the same cross section along the height of the tunnel. This does not affect packet drop. Only the equality of the masses of the liquid column and the proper wedge is necessary. On the Sun there is no "evaporation" from the shells of tunnels. "Steam" can enter the lifting elbow through a deep cell from the deep zone of the Sun, where the temperature is higher than on the surface.

Apparently, the Sun transforms gravitation into radiation. "In the atmosphere of the Sun energy transfer ... is carried out by radiation.In the upper atmosphere (chromosphere and corona) part of the energy is delivered by mechanical and magnetohydrodynamic waves, which are generated in the convective zone, but are absorbed only in these layers" (1, vol. 24, p. 151). Apparently, mechanical and MHD waves are generated during batch transformations in megatunnels, and then in the chromosphere and corona re-emit into "radiant" cosmic energy packets. This process allows you to make up for the loss of radiant energy on the Sun.

K. On the Earth, macrotunnelling at g = 9.80665 m / s 2 is associated with a nuclear magneton, a fine structure constant and a Bohr magneton. In the microworld, their equations include the Planck constant and the speed of light. The coefficient q = 4 / = 1.273. .. is associated with the diameters of the Earth: the equatorial - 12756.32 km, and the polar - 12713.55 km, i.e. the Earth is conjugated to the quadratures of 4 circles of the wedge of mass. The surface of the Earth "sweeps out" a square a day equal to its 4 large circles. Considering the above, but contrary to the opinion that "the Year is not a" natural "magnitude, it was introduced by people" (7, Volume 1, p. 137), let us consider the relationship between the rotation of the Earth and cosmic energy packets outside the Sun.

The year lasts 31556925.9747 s, and 365.24219879 sunny days correspond to 366.24219879 the star day of the Earth. At the radius of the Sun, Rs = 696000 km and the speed of light c = 299792456.2 ± 0.8 m / s, during the time of the Earth's star day T = 86164,09054 s light passes the distance L = 2,583134434 · 10 15 cm, equal to the solar package of 37114,000 ... Rs in length.

Packages run about each other allegedly with a double speed of light. But this is the imaginary accelerated propagation of light with a doubled velocity Vy = 2 · c. The real uniform speed of packet spacing according to equation (2) is equal to the speed of light: Vp = Vy / 2 = 2 · c / 2 = c.

Classical physics allows us to consider this phenomenon of nature without violating the prohibition on exceeding the speed of light propagation. The difference in the speed of light in 2 times reflects the difference in energy characteristics in the cube. Therefore, energy can be compared from the position of imaginary accelerated and real uniform coordinates of packet formation. The imaginary 2-fold acceleration of the packets Ps reflects the ultimate energy transfer, which corresponds to a smaller (in the cube) uniform energy transfer by the Pw packets:



The dimension of the seven significant digits of the Pw packets is conjugate with the speed of light propagation c = 3.335640. . . · 10 -11 s / 1 cm and with the coefficient F = 333564.0 (derivative of the Faraday constant) used in the coordination of all world constants (4, p. 266). The double rate of energy transfer between the packets Pw = 2 · 33.3 ... Rs / T Less than the imaginary ultimate energy transfer between the packets Ps = 2 · 37114 Rs / T .

Invariance of the speed of light implies the invariance of the length of the Ps packets in the past, present and future. But astronomical measurements indicate a slowdown in the Earth's rotation by an average of 1.640 ms per 100 years. During the time t = 0.01640 ms, packets with the speed of light pass an additional 4.916 ... km per year. Therefore, each of 37114 packet intervals and the radius of the Sun, which is an energy marker of the length of the 1 interval, should grow by 4.916 ... km / 37114 = 13.24 ... cm / year. At the same time, the imaginary double accelerated rate of mutual growth of the radii of the Sun when the packets are scattered is Vy = 2 · 13.24 ... cm / year.

According to the formula (2), the real uniform double speed of mutual growth of the solar radii Vp = Vy / 2 = 2 · 13.24 ... / 2 = 13.24 ... cm / year is equal to the growth of the diameter of the Sun, and single - to the growth of the radius of the Sun At 6.62 ... cm per year. This determines the invariance of the number of 37114 Rs intervals in growing Ps packets and indicates the "birth" of the Sun-Earth system and its initial energy packets in the microworld. The planetary model of an atom admits this.

In Table 1 , in the metrics of the Sun-Earth system (S1), the parameters of the S1-4 systems are shown with a decrease in the solar radius Rs = Rn1, the Earth's time T1 and the Ps = P1 packet by 12 orders of magnitude. They correspond to packets Pw, packet lengths Lp, Lw, growth Sn of radii of nuclei Rn, energy transfer W = T / Lw. Only the first three significant digits and the number of orders are given. The speed of light, expressed as c / Rs and c / cm, is equal to the length of the packets Lw4 = Pw4:

C = 2,321,606 ... s / Rs = Lw4 [2,321605 ... cm] (16)

C = 3.3356409 ... -11 s / cm = Pw4 [3,3356406 ... -11 Rs] (17)

The length of the Lp2-4 packets is smaller than the radii of the Rn2-4 nuclei that form them. This seems unrealistic. But in their own coordinates of time reference T2-4 and radii Rn2-4, the length of Lp2-4 packets is larger than the Rn2-4 radii. For example, packets P3 form nuclei with a radius of Rn3 = 6.96-14 cm. At T3 = 8.61-20 s, the packet length is Lp3 = c · T3 = 2.58-9 cm, and the number of radii of the nucleus n3 in packet P3 is Lp3 / Rn3 = 37114 Rn3. As a consequence, for us in the S4 system, the real energy transfer rate W4 is equal to the energy packet P4.

The radius of the nucleus Rn3 is equal to the radius of the nucleus of the atom 10 -14 cm. For us, the length of the packet L3 = 2.58-33 cm is equal to the fundamental length of 10 -33 cm. But in the proper metrics of the system S3, the packet length Lp3 = 2.58-9 cm equals the radius Atom of 10 -9 cm.

The above explains the reason for the red shift. With an annual slowdown of 1 turn T Earth for a time t the growth of packets P4 to packets of Ps lasts: T / t = 5.25 ... billion years. Hence, for example, the radius of the Sun 2.6 ... billion years ago was 2 times less, and the day is 2 times shorter.

In Fig. 7 shows the space packets Ps then and now in conjugation with electromagnetic waves at a constant speed of light. Earlier packs were shorter and they contained a certain number of waves. For clarity, 1 wave is shown. Now the packages are 2 times longer and contain 2 waves.

Observing the universe from a distance of 2.6 ... billion light years, we see events in which time went 2 times faster. As the packets approach the Earth, the accelerated rate of time fixed in the light stream in the form of light waves "frozen in", into packets, slows down to a real time for us. As a result, past packets and all waves of light, "frozen in" them, are synchronously stretched to the length of the packets at the present time. In this case, a relativistic decrease in the frequency of light should be observed in 2 times, expressed in redshift.

The initial packets form zatomic nuclei with a radius of Rn4 = 6.96 × 10 -26 cm. The dimension of the first three digits of the growth rates of Sn1-4 is equal to the Planck constant h = 6.626176 ... · 10 -34 Js. Their absolute equality corresponds to a slowing down of the Earth's rotation by 1.64062 ... ms per 100 years. Since 1 J reflects the transport of matter by 1 m, when the matter is transferred by 1 cm, Planck's quantum of action is h = 6.626176. .. · 10 -36 sJ · s in digital expression is equal to the growth of Sn4 = 6,626176 ... · 10 -36 cm / year. Consequently, the smallest (s) growth rate of the nuclear radius n4 is Ss = Sn4 / 31556925.9747 s = 2.099753 ... · 10 -43 cm / 1 s.

The growth of nuclei is not infinite. The rate of their growth can not exceed the speed of light c = 2.99 ... · 10 10 cm / s. The lowest growth rate Ss of n4 nuclei is less than the speed of light in 1.42 ... · 10 53 times. Hence, the maximum permissible radius of the core of the universe is Rn4 · 1.42 ... · 10 53 = 9.93 ... · 10 27 cm, i.е. 10.5 ... billion light years. The ratios Ss / c = Rn4 / R of the Universe = 7.00 ... · 10 -54 are equal to the cosmological constant Describing the energy density and the vacuum tension for a particular cosmic force of attraction at And repulsive forces at

The growth of nuclei and cosmic energy packets causes a proportional expansion of all structures of our universe. This is of great importance. For example, the Moon moves away from the Earth on average by 3.66 ... cm per year, because The average distance between the centers of the Earth and the Moon is 1.81 ... times less than the radius of the Sun, which grows by 6.62 ... cm per year.

The earth is also growing. The Earth's radius is 109.2 ... times less than the radius of the Sun and its radius grows by an average of 0.06 ... cm per year. But the Earth rotates unevenly and there are periods of acceleration of its rotation. During these periods, the distance from the Earth to the Moon is reduced, and the Earth is compressed, i.e. The Earth's rotation, its dimensions and Earth-Moon distance vary synchronously.

Fluctuations in the variation of the distance from the Earth to the Moon and the fluctuations in the Earth's rotation reflect the periodic contractions of the Earth. The growth and periodic contractions of the Earth can cause earthquakes and therefore can serve as seismic precursors. The date and intensity of earthquakes can be determined by the simultaneity of the fluctuations in the slowing down of the Earth's rotation (which is 0.0164062 ... ms / year on average) and the fluctuations in the increase in the distance from the Earth to the Moon (which is 3.66 ... cm / year or 0, 01 cm / T average). This can be done by comparing the annual fluctuation of W with the average increase in the distance from the Earth to the Moon, Si = 0.01 cm for the stellar day T :

Si = W / N (18)

Where W is the measured annual growth of the Earth-Moon distance;

N - 366, ... is the number of star day T In the year.

For 1 revolution T (Analog of period 1 in the mass wedge package), the growth of the Earth-Moon distance Si = 0.01 cm is 1/100 of 1 cm, i.e., equal to the width 1 of the discrete energy level h in the packet with H = 1 cm and the number Ni = 100. The daily measurement of Si and T Will refine the forecast of earthquakes on the fluctuations of these quantities in the special (double) planet of the Earth-Moon Solar System.

At the same time, it is necessary to observe the thermal regime of the seas and oceans, which also affects small changes in the size of the Earth. The rise in temperature of the oceans and seas causes the inevitable growth of the Earth due to the temperature increase in water volumes, and this delays earthquakes caused by an increase in the volume of the globe. But ultimately this delay can be unfavorable when the Earth's rotation is accelerating and the Moon is approaching the Earth. During these periods, the Earth contracts. But the temperature of the water may not decrease, water will not reduce the volume and will not compensate for the increase in the tectonic stress of the earth's crust. In this case, the strongest earthquakes are expected.

L. Accelerated (double velocity) energy transfer by packets Pw1 = 2 · 33,35640 ... = 66,71 ... Rn / T1 is conjugated to the proportionality coefficient G = (6.673 ± 0.003) · 10 -8 cm 3 / g · With 2 , reflecting the accelerated function of gravitation (time in square). The degree of 10 -8 in G and in the uniform energy transfer rate W1 = 3,7114 · 10 -8 s / cm is the same (time in the first degree). Therefore, the extraction of the root from G transforms the hidden accelerated functions of the transfer of energy and gravitation into real uniform ones.

According to Table 1, all parameters of all packets are conjugate with the speed of light, and the length of the packets In Table 2, between subsystems sC and S2 for 1 revolution T Packages Lp = 2,58314434 · 10 -4 cm, equal to Hence, the hidden accelerated gravity function is equal to the dimension of the uniform speed of light and packets propagation:



From the position of our space-time in the subsystem sA, the relationship between the length of the packets and the radii of the nuclei is violated, and starting from the subsystem sB, the packet lengths Lp are smaller than the radii Rn that form them. Therefore, against the background of relativistic specificity in the evolution of energy packets in the Universe, the speed of light in equation (19) is supposedly less than its invariant value c = 2.997 ... · 10 10 cm / s in any space-time metrics.

Reduction of packages is also evident in supersystems, which are larger than the solar system. Thus, in our metrics the packet length Lp + = 2.58 + 21 cm is larger than the same packet length in the proper metrics of the supersystem S +: Lp + = 37114 · Rn + = 2.58 + 18 cm. From this it follows that from the position of our metrics Packets of Lp + are formed with excess of the speed of light, which is unrealistic. For us, only the Earth-Sun form packets of real length.

Limit (l) the length of the packet can not exceed the radius of the core of the universe and is equal to Ll = 9.93 ... · 10 27 cm. It is formed by a nucleus with a limiting radius Rl = Ll / 37114 = 2.67 ... · 10 23 cm, Which is larger than the radius of the Sun in 3.84 ... · 10 12 times. Accordingly, for the time of the star day of the Earth, T1 = 86164,09054 s, the time Tl = T1 · 3.84 ... · 10 12 = 3.31 ... · 10 17 s.

The light passes through the radius Rl, equal to the length 1 of the interval of the length of the packet Ll, in time tl = Tl / 37114 = 8.93 ... · 10 12 s. Electromagnetic waves propagate within a time rl in the limiting radius Rl with the maximum possible speed of light c = Rl / ml = 2.99 ... · 10 10 cm / s. This means that from this moment the speed of light will block the further growth of the packets.

Starting with Rl, growing kernels catch up with the invariable size of the packets being formed, and the core of the universe is compared with the length of its packets. Therefore, the evolution of packets ends on the sphere of the core of the universe with their "zero" length with the number of 37114 intervals hidden in them equal to the radius of the core of the universe.

In Fig. 8 shows the circle of the evolution of matter. The solid semicircle is the phase of growth S of the nucleus n4 to the size of the core of the universe for 10.5 ... billion years. The dashed semicircle is the compression phase C of the Universe core for the next 10.5 ... billion years to the size of the nucleus n4. Together with the two-phase evolution of the universe with the speed of light, the clock system rotates clockwise. Two points of the circle reflect the phase change. The lower point is on the sphere of the nucleus n4, and the upper point is on the sphere of the core of the universe. The left and right features of the circle are 1/2 phases of the evolution of the nuclei, in which the "solar system" (S1) is located by "age".

At the lowest point, at the time of the transition of the lowest compression rate Cs of the nuclei n4 to the slowest growth rate Ss, the values ​​of Cs = Ss = 2.09 ... · 10 -43 cm / s are identical. With the growth of n4 nuclei, the rate of their growth continuously increases, and when the size of the core of the universe is reached, it is compared with the speed of light. In this case, the length of the packets first grows to the limiting length Ll with the nucleus Rl, where the rate of their growth is compared with the speed of light, and then, with the fixed blocked length, Ll is compressed to zero on the sphere of the core of the universe.

At the upper point, at the instant of transition of the highest (g) growth rate Sg of the Universe core to the highest compression rate Cg, the values ​​of Sg = Cg = 2.99 ... · 10 10 cm / s are identical - the velocities of light are equal. When the core of the Universe is compressed, its compression rate decreases continuously and when the nuclear size is reached, n4 is compared with the speed Cs = Ss. Packages, starting with their zero length on the sphere of the core of the universe, expand (expand) to the radius Rl, where the rate of their compression-compression is equal to the speed of light for c = Sg = Cg, and then decrease to the sphere of the nucleus n4.

However, the one-round evolution of our universe is impossible. In the transition to the compression phase, in which the core of the universe contracts from the sphere to its center, the "direction" of the evolution of the nucleus must change to the opposite, with the course of time counter-clockwise. Since time enters into the uniform metrics of expanding or contracting space-time, the one-stage course of time, both in and counterclockwise, in the one-dimensional evolution of the universe is impossible.

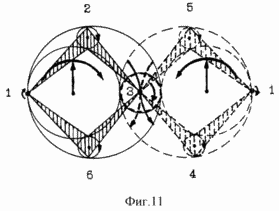
M. In Fig. 9 shows two circles of the evolution of matter, in which the course of time is reversed. The left circle (clockwise rotation) is the expansion phase of the universe. The right circle (counter-clockwise rotation) is the latent phase of the compression of the universe. In the zone of tangency of circles, matter passes from the region of the expanding universe into the invisible region of the shrinking universe and vice versa. Objects that enter circles have the same rotation vectors or reversal of their structures either clockwise or counterclockwise (clockwise in the drawing).

The two-round evolution of matter corresponds to the concept of Black Holes as invisible components of binary stellar systems in which one component is the ordinary visible Star and the other is an invisible cosmic object - the Black Hole. A rotating Black hole has a limited ergosphere zone. The objects of the ergosphere have a moment of rotation that coincides with the angular momentum of the Black Hole. In Fig. 10 matter flows from an invisible black hole into a visible optical star and vice versa (1, vol. 29, p. 82).

Since the lowest packet compression rate is realized on the sphere of the nucleus n4, the packets can not penetrate into the core of n4. In view of the zero length of the packets on the sphere of the core of the Universe, they can not, as well as from the Schwarzschild sphere, leave the core of the Universe. For this reason, the visible expansion and invisible compression of the nuclei occurs in the "ergosphere zone of the entire Universe" between the two Black Holes: the spheres of the n4 nuclei and the Universe. According to the theory of black holes, the relativistic gravitational contraction (collapse) of stars confirms the possibility of compression of the core of the universe.

But the two-phase-two-circle evolution of the Universe is unrealizable, for in the zone of tangency of circles, matter can not move from circle to circle in different metrics of space-time: when going from left to right-hand circle - at the moment of maximum extremum of metrics, and at the moment of transition from right to left Circle - at the moment of minimum extremum of metrics.

This contradiction does not exist for a four-phase two-circle evolution of space-time in two equal symmetric circles, each consisting of two semicircular phases (Figure 11). Objects of circles, with the same dimensions, vectors and rotations of rotation or reversal of their structures, pass over opposite sinusoids from points 1 to a single point 3 in the zone of tangency of circles from one phase to another. Different phases of the sinusoid are in different circles. It is understood that the spaced points 1 are also a single point of tangency of the circles.

The left circle (clockwise rotation) is our World, and the right circle (counterclockwise rotation) is Antimir. Matter-antimatter for 21.0 ... billion years passes the length of the sinusoid between points 1. The phase of the expansion of the universe lasts 10.5 ... billion years (the upper solid lines - points 1, 2, 3). The other half of the sinusoid is the compression phase in the right circle of the Antivel (the lower dotted lines are the points 3,4,1). From the position of the right circle, the same: the upper dotted lines (points 1, 5, 3) - the expansion phase, and the other half of the sinusoid is the compression phase in the left circle (the bottom solid lines are points 3, 6, 1).

Circles of Peace and Antimir are closed from each other. However, they are one in infinite Cycles of expansion-compression of real and latent space-time with a duration of 42.0 ... billion years, in which "everything returns to normal." The hidden accelerated functions of each circle appear in another circle in the form of a compression force (gravity force) against the background of the growth of the nuclei of this circle, which is expressed in the expansion of space and in the elongation of the rotation time of their structures, i.e. In their relativistic slowing down of the rate of rotation (the rate of time).

Since earlier the second reflected only the second division of a degree, and now is used for the second division of the hour, the "packet time" of forming packets at 37114 Rn1-4 for 1 axial rotation of T1-4 relative to the stars is related first of all with an unchanged number of 360 degrees - 3600 '' seconds. But as a unit of time, the packet time is related to T1-4 = 86164,09054 s when the packet rotation time is slowed down t1-4 = 0.0164062 ... ms in 1 own year, because according to Table 1 in the metric range of S1-4 systems T, Rn, Sn and P differ by 36 orders of magnitude only by absolute values. This causes the batch relativistic constant T / t = 5.25 .... Billion of its own years in S1-4 systems.

Starting from the relativistic constant T / t, all systems S1-4 are at point 2. Therefore, the Solar system (S1) consists of Atoms (S3). The growth of the nuclei of all systems has passed the ½ time evolution to the age of the universe 10.5 ... billion years at point 3. In this case, all the nuclei continuously increase from point 1 to point 3. The length of the packets first increases from point 1 to the nucleus with the limiting Radius Rl, and then compressed to zero at point 3.

The radius Rl = 2.67 ... · 10 23 cm = 283014.3 ... light years is also a relativistic value. Its spatial metric of 2.67 ... · 10 23 cm is located between the points 2 (radius Rs = 6.96 × 10 10 cm) and 3 (the radius of the core of the universe = 9.93 ... 10 27 cm), and the time The metric of 283014.3 ... light years is between points 1 and 2, because at point 2 the relativistic age of all systems is 5.25. .. billion years. Since in FIG. 11, it is impossible to designate a space-time radius Rl as a single point, where a change in the growth-contraction of the length of the packets is fixed, then the length of the packets is shown by abstractly shaded expanding and contracting chords with respect to point 2.

In our rotating universe, the phase transitions of the highest growth rate-compression of nuclei at point 3 on the sphere of the nucleus of the universe and the highest rate of packet growth and compression at the limiting nucleus with radius Rl occur at the same rate of exchange interaction equal to the speed of light c = Sg = Cg.

Phase transitions of the lowest rate of growth-shrinkage of nuclei at points 1 (sphere of the nucleus n4) in accordance with the quantum of Planck's action occur with the identical exchange interaction rate Ss = Cs = 2.099753 ... · 10 -43 cm / 1 s.

In our space-time, the metrics of the Solar System (S1) and the Atom (S3) differ in absolute values. Therefore, our day lasts longer than the atomic year. But when measuring space-time by means of a packet time, in which the values ​​37114 Rn and T / t are constants, the metrics are S1 = S3. The possibility of determining the age of the Earth from the decay time of the radioactive elements of the atom confirms this.

The packet time is associated with an increase in 1 interval Si = 0.01 cm at Ni = 100 in a 1 cm package in the Earth-Moon space, i.e. At 3.66 ... cm for 366, ... Star day T In the year. In this case, 360 ° degrees and 3600 '' seconds of 1 packet turnover T Are associated with 36 orders covering the range of space-time metrics of systems S1-4.

The Universe, the Stars, the Atoms are a single conjugated system. Batch time 1 axial revolution T Is a universal relativistic time unit for the formation of energy packets with a number of Ni = 100 and 37114. Systems S1-4 are equivalent spatio-temporal energy structures. They do not form and do not disappear. They exist eternally in endless cycles of evolutionary transformations.

H. To release the packet energy of the Universe, in particular the force of their compression C (gravity g), it is possible in a closed tunnel in which the working medium does not leave into free space. The transformations in it can be described from the position of strength, although "The idea of ​​force is not very suitable for quantum mechanics, the idea of ​​energy is more natural there" (7, vol. 1, p. 252). Since packet tunneling relies on local average forces f as the action of hidden discrete impulses of forces fi, the combination of the idea of ​​force and energy, in the form of energy-impulses Ei, simplifies the consideration of practical problems.

A closed tunnel is a device known as a heat pipe of gravitational action (Figure 12). The liquid evaporates below the tube, and vapor condenses on top. The central part of the pipe is a neutral zone. The heating zone is the working section, which corresponds to the requirement of boiling out the wedge of the mass when the liquid particles fall.

Circulation in the heat pipe is not associated with an unbalanced vessel. The following principle of its operation is adopted: "The presence of a constantly operating pressure drop ... ensures a continuous flow of steam along the heat pipe, the more intense the pressure of steam will be, the greater the difference between the density of the saturating vapor of the liquid at Given temperature N and the density of the liquid itself , Ie, heat transfer will be more effective if expression 1 - N / (6, p.25), an analogous dependence is shown in an unbalanced vessel, where as the difference in liquid / vapor density increases, the rise time of the vapor particles decreases, and as a result, the efficiency of the work of the bypass increases, tending to unity.

However, in experiments, the difference in temperature over the height of the heat pipe does not affect the heat flux. This phenomenon was discovered, but not explained: "In the heat pipe, the heat transfer Q in the first approximation does not depend on the temperature drop" (6, p. 24). Contrary to the theory of temperature differences and pressures, "... the maximum axial flow that can be obtained at a given evaporator temperature turns out to be ... independent of the intensity of the heat sink" (3, p. 293). High heat fluxes under isothermal circulation are noted (2, p.66), which also facilitates starting the pipe in the circulation mode (2, p. 106).

Description of the gravitational heat pipe from the position of the tunnel with unbalanced bends of the annular column of liquid and the vapor column inside it eliminates the paradoxes of circulation of the two-phase working body in the heat pipe. In this regard, the use of the tunnel as a heat exchanger is its attendant possibility.

A specific thermodynamic equilibrium is realized in the tunnel. Usually the diffusion of liquid molecules into the saturated vapor phase occurs at the phase boundary together with the countervailing diffusion of vapor molecules into the liquid. In the tunnel, the molecules of liquid and vapor are introduced into the inverse phases in different zones without the counter-diffusion of the molecules of vapor and liquid, and therefore the energy losses during the process of return-body return during evaporation and condensation are minimal. For this reason, in a heat pipe "... heat is not expended on heating the liquid, but on cooling compensation" (6, p. 9). Consequently, the smaller the role of the tunnel as a heat exchanger, the less energy is needed to maintain the circulation process. Hence, the heating zone in the heat pipe corresponds to the zone of compensation for heat losses in the tunnel.

The theory of heat pipes differently explains the reason for the slowing down of the fall of the liquid: "At high steam flow rates, its interaction with the counterflow of the flowing condensate is significant.As a result, in any cross section of the heat pipe, a complex diagram of the velocities of the liquid and vapor molecules takes place. 6, page 21). The slowdown of the "flow" of liquid in the tunnel is a consequence of quantization, i.e. Packet tunneling.

To isolate the energy of the compression force of space-time (gravity g), certain conditions are necessary. For this purpose, the vapor condensation zone can be made in the form of an expansion vessel in which an electric current is generated by magnetohydrodynamic (MHD) energy conversion of the steam (FIG. The pressure drop in it facilitates the launch of the tunnel and the maintenance of a specific circulation associated with the release of energy. The expansion tank does not affect the batch drop in the liquid in the tunnel. The neutral zone between the tunnel heating zone and the reservoir may be absent.

In the MHD generator, conductive pairs must flow. The electric current is carried out by pairs of alkali metals. These metals are also used as fillers for heat pipes.

Table 3 shows the main parameters of the sodium filling tunnels with the height H of the working zone of the tunnels 100, 200 and 300 cm at heating temperatures 800-1300 ° C. The released energy Ef increases with increasing temperature and height of the tunnels, and the efficiency of the work of bypassing two-phase sodium Slightly decreases with increasing temperature of heating of tunnels. However, at specific temperatures, the efficiency increases with the height of the tunnels. At different heights and heating of tunnels, the efficiency corresponds to the ratio Ef / Mb - the energy Ef released per sec of energy E to the vapor mass Mb boiled out for 1 s.

For example, at H = 100 cm, the energy Ef increases from 0.006 J / s (800 ° C) to 0.963 J / s (1300 ° C) with a decrease in efficiency from 0.989 to 0.927. At the same time, the steam flow rate W at the exit from the tunnel decreases slightly from 4.42 m / s to 4.26 m / s, the velocity of the drop of the liquid v increases from 2.0 cm / s to 11.6 cm / s, and predetermines the value Ef the mass of the wedge Mc, which increases from 0.035 kg to 0.908 kg.

In the above example, the efficiency factor reflects only the work of bypassing two-phase sodium in a gravitational heat pipe-tunnel. In this case, the total entropy of vapor and liquid is not taken into account in phase transitions. The limitations of circulation due to the thermophysical properties of sodium are not considered, and irretrievable dissipation of heat into the external environment. The losses due to MHD conversion of the kinetic energy of the sodium vapor stream are also not taken into account.

Since irrecoverable energy losses are mainly due to entropy of the phase transitions of the sodium working fluid, the energy released in the MHD generator will exceed the energy expenditure for maintaining two-phase sodium circulation in the heat pipe-tunnel.

Thus, the invention improves efficiency in use.

Industrial applicability.

The invention can be used in industry to generate electricity.

BIBLIOGRAPHY

1. The Great Soviet Encyclopedia, 3rd edition, 1969-1978.

2. Dan P. et al. Heat Pipes, M. Energia, 1979.

3. Devverall D. Mercury as a coolant of heat pipes. Sat: Heat Pipes, M. Mir, 1972.

4. Dumond D. Exact measurements of universal physical constants. Sat: Science and Humanity, M. "Knowledge", 1964.

5. Einstein AJ Franklin Institute, volume 221, 1936.

6. Eliseev V. et al. What is a heat pipe? M. 1964.

7. Feynman R. et al. Feynman lectures on physics, M. Mir, 1967.

CLAIM

1. A method for producing electric power, comprising forming a closed sealed vessel, placing a transducer inside it, including electrodes, current collectors, filling the cavity of the vessel with an alkali metal, and then heating the vessel to allow circulation of the alkali metal and for further formation of electric current on the electrodes with its simultaneous Feeding to the consumer load, characterized in that sodium is used as an alkali metal, rigidly connected and co-axially located pipes of different diameters and lengths are used as a sealed vessel, and a converter is used in the tube of a larger diameter and shorter length, which uses an MHD generator Installed with a gap in relation to the walls of the cavity of the pipe, the electrodes of which are disposed in the longitudinal direction and with the possibility of forming a nozzle, the smaller section of which is directed towards a pipe of smaller diameter and longer length, before cleaning the interior walls with alkali metal to be wettable by sodium , The sealed vessel is placed in a vertical position with a smaller diameter pipe placed on top and the vessel is preheated to a temperature of 150 ° C, filling the cavity of the vessel is carried out through a tube at the end of the pipe that is less than the diameter of the pre-melted sodium at a temperature of 150 ° C in the amount of 110-115 G, then the vessel is evacuated to a pressure of 10 -8 to 10 -10 mm Hg. Art. And sealing the through passage, and before the subsequent heating of the vessel, the latter is rotated through an angle of 180 ° into another vertical position for placing a larger diameter pipe on top, the subsequent heating being carried out simultaneously with the supply of an electric current generator to the electromagnet; simultaneously heating the sodium to a temperature of 800 to 1300 O C to allow circulation of liquid and formed sodium vapor and evaporation of sodium over the entire length of a tube of smaller diameter from the annular layer of liquid sodium, and the formation of an electric current generator on the electrodes of an MHD generator is obtained by the interaction of sodium with a gravitational field due to the simultaneous circulation of liquid sodium and sodium vapor In pipes of different diameters and lengths and passing the flow of steam through the nozzle of the electrodes, after the formation of electric current on the electrodes, the spent sodium vapor is condensed and the condensate drains from the larger diameter pipe into the smaller diameter pipe to form a closed conversion cycle.

2. An apparatus for producing electric power, comprising: a converter arranged in the cavity of a closed sealed container filled with an alkali metal, adapted to be able to communicate with the load of the consumer and comprising electrodes, current collectors, and means for heating the vessel to allow circulation of the alkali metal, That a sodium is used as the alkali metal, the closed sealed vessel is designed as pumped-out and in the form of rigidly connected and co-axially located pipes of different diameters and lengths. In the tube of a larger diameter and shorter length, a converter is used, which uses an MHD generator installed with a gap with respect to Walls of the cavity of the tube, the electrodes of which are arranged in the longitudinal direction and with the possibility of forming a nozzle, the smaller section of which is directed towards a pipe of smaller diameter and longer length, the means for heating the vessel is in the form of a spiral wound around the entire length of the surface of the tube of smaller diameter, The power supply of which is simultaneously connected to the magnet of the MHD generator.

3. The device according to claim 2, characterized in that it has a process tube installed at the end of a pipe of smaller diameter to fill the cavity of the pipe with sodium through it, and the pipes and the process tube are made of steel, while in a pipe of smaller diameter, the internal diameter is 24, 0 - 35.0 mm, length 1000 - 3000 mm, wall thickness 1.5-2.0 mm, in a larger diameter pipe diameter is 150 - 200 mm, length 250 - 300 mm, wall thickness 1.5 - 2.0 Mm, and the internal diameter of the process tube is 5.0 - 7.0 mm, length 50 - 100 mm, wall thickness 0.7 - 1.0 mm.

4. The device according to claims 2 and 3, characterized in that it has brackets for securing the protective casing of the MHD generator and the current collectors and current insulators located therein.

print version
Date of publication 09.01.2007гг