| Start of section
Production, amateur Radio amateurs Aircraft model, rocket-model Useful, entertaining |
Stealth Master
Electronics Physics Technologies Inventions |
Secrets of the cosmos
Secrets of the Earth Secrets of the Ocean Tricks Map of section |
|
| Use of the site materials is allowed subject to the link (for websites - hyperlinks) | |||
Navigation: => |
Home / Physics / Experiment / |
|
ON POSSIBILITY OF MOVEMENT OF THE CLOSED MECHANICAL SYSTEM
FOR THE ACCOUNT OF INTERNAL FORCES
![]()
Leave a comment

The author of the article does not come up with new laws and in no event
Do not try to violate the acting.
Is it possible to move a closed mechanical system, which is not acted upon by external forces?
There is a theorem on the amount of motion:
The time derivative of the momentum vector of a system of material points is equal to the principal vector of all external forces acting on the system.
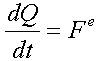
Several corollaries follow from this theorem:
- Internal forces do not directly affect the change in the amount of movement of the material system.
- If the principal vector of all external forces acting on the system is zero, then the vector of momentum of the material system remains constant in magnitude and direction.
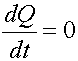
- If the projection of the principal vector of all external forces applied to the system to some fixed axis is zero, then the projection of the amount of motion of the material system on this axis remains constant.
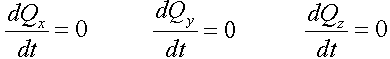
Corollaries (2.3), in fact, are called the law of conservation of momentum.
For a closed system, that is, a system that does not experience external influences, or in the case when the geometric sum of the external forces acting on the system is zero, the law of conservation of momentum holds.
In this case, the amount of movement of individual parts of the system (for example, under the influence of internal forces) can vary, but so that the quantity
![]() Remains constant.
Remains constant.
The law of conservation of momentum can not be violated. Impossible!
And it can not be avoided.
But can it be used to solve a problem that at first glance contradicts this law?
I bring to your attention the following scheme of reasoning:
The displacement of the body shown in Fig. 1 can not be realized without the participation of another body in this process.
Since the amount of motion of the body, in the projection on the coordinate axis, is constantly changing and differs from zero.
Fig. 1
Linked together inextricable and inextensible communication of the body can move as shown in Fig.2.
With this movement, the bodies will move along circles whose radii are inversely proportional to their masses.
This is a consequence of the law of conservation of momentum.
In this case, the total momentum of the system is zero.
Fig. 2
Here's how it would look in the case of two "real" objects (Fig. 3).
Let's call one of them "corps", and another - "working body", or "working substance".
Fig. 3
If two working bodies (having the same masses and speeds of relative displacement) take part in the relative movement inside (around) the hull (Fig. 4), then the body will not acquire a rotational motion.
In this case, the total momentum of the two working bodies in the projection onto the X axis is zero.
Therefore, the momentum of the hull, in the projection on the same axis, will also be zero.
The body will perform reciprocating movements relative to the center of mass of the entire body system.
Moving the hull will be carried out along one axis of the "absolute", fixed coordinate system.
In the coordinate system associated with the body, the working bodies move around the circumference.
In a fixed coordinate system, the working bodies move along an elliptical trajectory.
The kinetic energy of the components of the mechanical system can be attributed to the conversion of other types of energy included in the closed system.
That is, it is possible to organize relative movements of system components at the expense of internal forces.
In this case, the center of mass of the whole system will always remain in place, that is, do not change its coordinates (or move rectilinearly and evenly).
Fig. 4
We will modify the system shown in Fig.
We use not a "point" body, but a working mass uniformly distributed over a certain section of the trajectory (Fig. 5).
Fig. 5
With uniform relative displacement, the "body" and the "working mass" will move along circles whose radii are inversely proportional to their masses (Fig. 6). Under the radius of the trajectory of the working mass, it is necessary to mean the radius of the trajectory of the motion of the mass center (CM) of the working mass (the red dot in the figure).
Fig. 6
Here's how it would look for a "real" system of bodies (Figure 7)
Fig. 7
Similarly (Fig. 4), it is possible to use several working masses in the system for equilibration of the angular momentum. (Fig.8)
Again, the center of mass of the entire system is stationary.
Fig. 8
And what happens if the working mass uniformly and inseparably fills the entire trajectory of displacement? (Fig.9) Nothing! The center of mass of the working mass coincides with the center of mass of the shell. The total momentum of the distributed working mass in the projection on all the coordinate axes is zero. Therefore, the momentum of the hull is zero.
The mass centers of the system components do not move relative to each other. The system is stably stationary. At the same time, we can give the moving working mass considerable kinetic energy.
Fig. 9
"Interesting" begins when we begin to stop the moving working mass at a certain point of the trajectory. (Fig.10)
We stop - this means, in this case, - a consistent "connection" of all the elementary particles of the working mass with the body.
That is, the particles of the working mass at a certain point of the trajectory successively acquire the speed of the hull, losing the speed of relative displacement. At the same time, the rest of the working mass continues to move until all of its particles gain the speed of the hull.
For example, moving some liquid along a closed trajectory, we suddenly begin to collect it in a container fixedly fixed in the body.
Fig. 10
In the animated drawing, red indicates the conventional CM of the working mass. Green - the trajectory of the movement of the CM in its relative movement relative to the "body."
The displacement of the radius vector of the CM of the working mass can be regarded as the displacement of a pendulum of variable mass and variable length. (In the coordinate system associated with the body.)
That's where the interesting task was defined:
- To calculate how the components of the system move?
Calculations led to the following result (Fig.11).
After the cycle of stopping the entire working mass is completed, the CM of the entire system is displaced relative to its initial position. The system moves in full accordance with the law of conservation of momentum!
It can be said otherwise : In order for the law of conservation of momentum to be satisfied, the center of mass of a given mechanical system must move.
The first calculation was made based on the law of conservation of momentum.
The second - with the help of the Lagrange equations of the second kind.
The results are the same.
In solving this problem, the internal interactions of the components of the system are not considered at all.
No collisions!
No forces of inertia!
Only the kinetic and energy state of the system.
Fig.11
Figure 11 adds a final, additional step - the reduction of the centers of mass of the hull and the working mass to one point. This is necessary to more clearly represent the entire cycle of motion, with the possibility of repeating this cycle. The red line in the figure indicates the trajectory of the movement of the CM of the whole system, the blue line indicates the CM of the hull.
Mathematical calculations describing this alleged phenomenon, you can see at: http://varipend.narod.ru
print version
Author: Sergey Butov
PS The material is protected.
Date of publication 23.12.2006гг




Comments
When commenting on, remember that the content and tone of your message can hurt the feelings of real people, show respect and tolerance to your interlocutors even if you do not share their opinion, your behavior in the conditions of freedom of expression and anonymity provided by the Internet, changes Not only virtual, but also the real world. All comments are hidden from the index, spam is controlled.