Start of section Production, amateur Radio amateurs Aircraft model, rocket-model Useful, entertaining	Stealth Master Electronics Physics Technologies Inventions	Secrets of the cosmos Secrets of the Earth Secrets of the Ocean Tricks Map of section
Use of the site materials is allowed subject to the link (for websites - hyperlinks)

EXTENSION OF THE UNIVERSE - LOCAL PHYSICS
(Experience in building a modern physical picture of the world)

V.M. Myasnikov

Saint-Petersburg State Electrotechnical University
them. VIUlyanov (Lenin) (LETI)
Ul. Prof. Popova, Building 5, St. Petersburg, 197376, Russia

Leave a comment

• Introduction
• Quarters. Quarter spaces
• Space is mass. The law of universal gravitation. Model of a material point
• Expansion of the Universe
• Expansion of the universe => local physics

UNIVERSE. THE DYNAMICS OF THE UNIVERSE. GRAVITATIONAL VACUUM. THE PRINCIPLE OF MAHA
PRINCIPLE OF RELATIVITY NEWTON

The case of the "internal" space of the material point considered is a good model of our universe. We are considering the universe here from the standpoint of the Newtonian theory of gravity, but taking into account the gravitational sphere of the universe.

So, let M - the mass of the universe, then its gravitational radius

,

Hereinafter referred to as the radius of the universe. From the law of gravitation for r << R we find the square of the velocity of gravity on the gravitational sphere

Location

Hubble's law with Hubble constant H (independent of r ) . Thus, distant galaxies are in a state of free fall under the action of gravitational forces. Hence, in particular, we can conclude that the so-called cosmological and gravitational redshifts should be of the same nature (in the following we show this also from other considerations).

Note also the gravitational attraction force for a test particle of mass m ' located at a distance r from a fixed reference point ( r = 0 ) and which, with respect to the reference point, is represented as the repulsive force, and the acceleration of the free fall of the test particle on the gravitational sphere of the Universe Is called Hubble ) for r << R

Is there a limit to the gravitational action of a body of mass m on other bodies? The test body of mass m 'is acted upon by the Newtonian force of attraction . In addition, it acts on the Hubble force . Total Strength

For small r, the Newtonian term predominates, and in the reference frame associated with the body m , the force F is the attractive force. With increasing r, the Newtonian force decreases, and the Hubble force grows, and for some r the force F is zero, and with a further increase in r the force F becomes the repulsive force. The distance at which the force F = 0 is called the antigravity radius of the mass (body) m

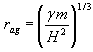
The existence of an antigravitational radius eliminates the so-called. The gravitational paradox taking place in the Newtonian universe explains the observable hierarchy of matter in the Universe, etc. In addition, our Universe is a unique object in which the antigravity radius is equal to the gravitational radius (Note that this circumstance significantly strengthens our confidence that we are on the right track, because our Universe, in its essence, should be a unique object where all "extremes" converge).

The attraction of the gravitational sphere, acting on any particle in the universe, as it stretches this particle evenly in all directions, which can be interpreted as the existence of negative pressure at every point of space in the universe, the latter, in turn, can be interpreted as the existence of a "substance" with a negative Density, evenly distributed in the universe. We called this " substance " a gravitational vacuum. The introduction of the gravitational vacuum allows us to abandon the "quasiclassical" gravitational sphere and use the classical Newtonian gravity in the Poisson formulation with the "vacuum correction"

Where Is the density of the substance, and Is the density of the vacuum.

The dynamics of matter and gravitational vacuum in the universe is completely determined by the density of matter. Let the homogeneous and isotropic Universe be uniformly filled with matter with constant density Or relative density , Where Is the Einstein critical density.

Let us select a sphere of arbitrary radius r centered at the reference point and denote by V and - velocity and acceleration of a particle of matter on the surface of a sphere and _{and - respectively, the velocity and acceleration of the "particle" of the vacuum on the surface of the sphere. The analysis of the equations of motion gives the following dependences of the velocities and accelerations of matter (and vacuum) as a function of the parameter :}

In the first case, the sphere expands ( V> 0 ), in the second and third - it contracts ( V <0 ). In view of the arbitrariness in the choice of the sphere, these conclusions extend to the whole Universe. Conditions ( 2 ) have a completely clear meaning. If the density Less critical ( <1 ), then the attraction of matter inside the sphere is insufficient to resist the attraction of the rest of the matter of the Universe (gravitational sphere), and an arbitrary selected sphere, and hence the Universe, expands. At the same time, there is no "first push", which the so-called " "Big bang", not required. If the density More critical, then on the contrary, the attraction of matter inside the selected sphere is greater than the attraction of the rest of the matter of the universe, and the selected sphere contracts. We draw attention to the fact that the transition from the expansion ( V> 0 ) to compression ( V <0 ) is possible only when passing through the parameter value = 1 , which, on the other hand, is impossible, because The acceleration is positive in this case. Happening = 1 , if possible, corresponds to the so-called. Singular state of the universe. (This contradicts the traditional Friedman model, which states that the case = 1 corresponds to the plane (Euclidean) model of the universe, see [ 3 ]. We affirm that this is a mistake. Interpretation of the solutions of the Friedmann equations for = 1 is directly opposite, this is the same, the mysterious singular state, and this singularity takes place not at the beginning of evolution and not at the end of it, but in the "middle").

Next, let us pay attention to the vacuum in ( 2 ). The gravitational vacuum expands or contracts together with matter, depending on the average density of the substance, because The velocities in the conditions ( 2 ) coincide in the direction. As regards accelerations, they are always opposite in sign and equal in modulus, which, as we have already mentioned, leads to negative pressures, forces opposing Newtonian gravity, etc. The necessity of the latter arises, for example, in cosmological models, in connection with the interpretation of the cosmological term . If we assume that the matter and the vacuum interact in the same way as in the dynamics of the universe, i.e. Their velocities are always the same, and the accelerations are always opposite in direction, then can not the forces of inertia be explained by the interaction of vacuum and matter?

Yes, it is possible, and we showed this in two ways. Firstly, strictly (within the framework of our model) we proved the Mach principle, that is, The forces of inertia really owe their appearance to the gravitational action of distant masses in the Universe or, what is the same, the forces of inertia are gravitational forces, and so the so-called Einstein equivalence principle holds. Secondly, we defined the " ideal inertial system " as a set of all imaginable inertial systems that arbitrarily move with constant velocities with respect to each other and are considered as ejectors , combining which with a gravitational vacuum, we determine the ef And p , which almost coincides with the classical ether, but is free from many (maybe all!) Of its shortcomings and, finally, we identify the ether with the Newtonian absolute space in which we formulate Newton's principle of relativity (equivalence):

The following two statements:

1. Body of mass m under the action of force 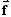Moves with acceleration Relative to the "fixed" absolute space;
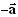2. Absolute space moves with acceleration Relative to the "immovable" body of mass m , while the body acts on the silt ;

- are equivalent ( "1 <=> 2." ).

Such a formulation of Newton's relativity principle includes all the laws of dynamics, in particular all three Newton's laws, and removes many of the "difficult" questions of Newtonian dynamics.

The model of the Universe considered above is based on the theory of the gravitational field, which is only a linear approximation of the equations of general relativity. A qualitative analysis of the laws of gravitation makes it possible to identify the most common components of such a model, such as expansion, Hubble's law, the hierarchy of matter, etc., but many details, related mainly to the evolution of the universe, remain outside the framework of this model.

LITERATURE

1. WRHamilton, Lectures on quaternions, Dublin, 1853

2. LD Landau, EM Lifshits . Theory of the field, "Science", Moscow, 1973.

3. Ya.B. Zeldovich , I.D. Novikov . The structure and evolution of the universe. "Nauka", Moscow, 1975

4. Cosmology. Theory and observation. "Peace". M., 1978

5. Problems of physics: classic and modern. Mir, Moscow, 1983

6. V. M. Myasnikov. Natural philosophy. (The book, about 400 pages. Unpublished)
7. V.Myasnikov. Expansion of the universe => local physics. Proceedings of Congress-98 "Fundamental Problems of Natural Science." Volume II. Series "Problems of the Universe" vol. 22. St. Petersburg, 2000

8. See also the site of the author http://Quater1.narod.ru, where the full text of the author's book "Natural Philosophy", this article and other articles of the author are given.

print version
Author: V. M. Myasnikov
PS The material is protected.
Date of publication 19.01.2005гг

NEW ARTICLES AND PUBLICATIONS
	The technology of manufacturing universal couplings for unbreakable, threadless, flossless connection of pipe sections in high pressure pipelines (video is available )
	Technology of oil and oil products cleaning
	On the possibility of moving a closed mechanical system at the expense of internal forces
	Fluorescence in thin dielectric channels
	The relationship between quantum and classical mechanics
	Millimeter waves in medicine. A New Look. MMV therapy
	Magnetic engine
	Heat source based on pump units