Measurement and construction (determination) of distances on a topographic map

Scales of cards
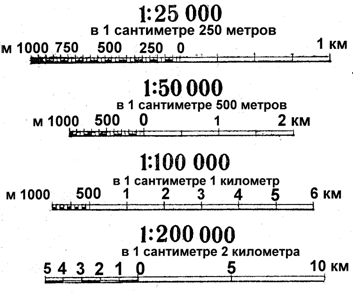
Fig. 1. Design of numerical and linear scales on topographic maps and city plans
The map scale shows how many times the length of the line on the map is less than the corresponding length on the terrain. It is expressed as a ratio of two numbers. For example, a scale of 1:50 000 means that all terrain lines are shown on the map with a decrease of 50,000 times, i.e. 1 cm on the map corresponds to 50000 cm (or 500 m) in the terrain.
The scale is indicated under the bottom side of the map frame in numerical terms (numerical scale) and in the form of a straight line (linear scale), on the segments of which the corresponding distances on the terrain are signed (Fig. 1). Here the scale value is also indicated - the distance in meters (or kilometers) on the terrain, corresponding to one centimeter on the map.
It is useful to remember the rule: if you delete the last two zeros on the right side of the relationship, the remaining number will show how many meters on the terrain correspond to 1 cm on the map, that is, the magnitude of the scale.
If several scales are compared, the larger one will be the one whose ratio on the right side is smaller. Let us assume that maps of the scale 1: 25000, 1: 50000 and 1: 100000 are available for the same section of the terrain. Of these, the scale 1: 25000 will be the largest, and the scale of 1: 100 000 is the smallest.
The larger the scale of the map, the more it shows the terrain. As the scale of the map decreases, so does the amount of terrain parts applied to it.
The detail of the image of the terrain on topographic maps depends on its nature: the fewer details the terrain contains, the more fully they are displayed on maps of smaller scales.
In our country and many other countries, the following are assumed as the main scale of topographic maps: 1: 10000, 1: 25000, 1: 50000, 1: 100000, 1: 200000, 1: 500000 and 1: 1000000.
The maps used in the troops are subdivided into large-scale, medium-scale and small-scale maps.
| Measurement on the map of straight and winding lines | |||
|---|---|---|---|
Map scale |
Name of the card |
Classification of maps |
|
By scale |
For the main purpose |
||
1:10 000 (in 1 cm 100 m) |
Ten thousandth |
Large-scale |
Tactical |
1:25 000 (in 1 cm 250 m) |
Twenty-five thousandths |
||
1:50 000 (in 1 cm 500 m) |
Five-thousandth |
||
1: 100,000 (in 1 cm 1 km) |
One hundred thousandth |
Medium-scale |
|
1: 200,000 (in 1 cm 2 km) |
Two hundred thousandth |
Operational |
|
1: 500,000 (in 1 cm 5 km) |
Five hundred thousandth |
Small-scale |
|
1: 1 000000 (in 1 cm 10 km) |
Millionth |
||
Measurement on the map of straight and winding lines
When measuring straight lines, the needles of the compass are set to the end points, then, without changing the solution of the compass, the distance is removed along a linear or transverse scale. In the case where the solution of the circulation exceeds the length of the linear or transverse scale, some integer number of kilometers is determined by the squares of the kilometer grid, and the remainder by the usual order in a linear or transverse scale.
Broken lines are conveniently measured by successively increasing the solution of the circulation with straight segments. The distance corresponding to the solution of the compass is determined by the order stated above.
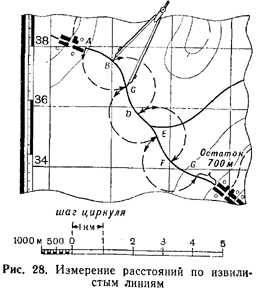
Measurement of the distances along the curves is made by the step of the compass. The length of the step of the compass depends on the degree of tortuosity of the line, but, as a rule, should not exceed 1 cm for accurate measurements. To eliminate the error due to deformation of the paper (map), the step length of the compass is preliminary checked along the kilometer grid line. To measure the distances on the map using the curvimeter, you must first (by rotating the wheel) set the arrow to zero (initial) division, then roll the wheel with uniform pressure from the initial to the end point. It should be noted that when the curvimeter is advancing, the count of the track increases, but does not decrease; Otherwise the curvimeter should be rotated by 180 °. If the scale of the curvimeter is signed in kilometers, the distance obtained is read directly from the scale.
If the scale of the curvimeter is signed in kilometers, the distance obtained is read directly from the scale. If the scale division is given in centimeters of the wheel path on the map, then the number of divisions obtained must be multiplied by the division price. To avoid errors, the price of the division is recommended to be determined by the control measurement along the kilometer grid line.

When measuring straight lines, the needles of the compass are set to the end points, then, without changing the solution of the compass, the distance is taken along the linear or transverse scale:
- Determination of distances on a linear scale by means of a compass When the circulation solution exceeds the length of a linear or transverse scale, some integer number of kilometers is determined by the squares of a kilometer grid, and the remainder by the usual order in a linear or transverse scale. Broken lines are conveniently measured by successively increasing the solution of the circulation with straight segments.
- Measurement of distances by way of increasing the solution of the circulation The distance corresponding to the solution of the compass is determined in the order described above. Measurement of the distances along the curves is made by the step of the compass. The length of the step of the compass depends on the degree of tortuosity of the line, but, as a rule, should not exceed 1 cm for accurate measurement. To eliminate the error due to the deformation of the paper (card), the length of the compass pitch is preliminarily checked along the kilometer grid line.
To determine the distance between the points of the terrain (objects, objects) using a numerical scale on the map, you have to measure the distance between these points in centimeters on the map and multiply the obtained number by the scale value.
For example, on a 1: 25000 scale map, measure the distance between the bridge and the windmill with a ruler (Fig. 2); It is equal to 7.3 cm, multiply by 250 m by 7.3 and obtain the required distance; It is equal to 1825 meters (250х7,3 = 1825).
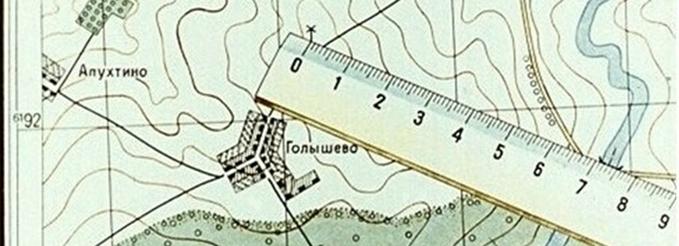
Fig. 2. Determine the distance between points on the map using the ruler.
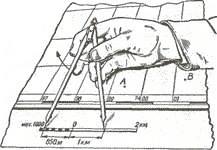
A small distance between two points along a straight line is easier to determine using a linear scale (Figure 3). To do this, a compass meter is sufficient, the solution of which is equal to the distance between the given points on the map, to attach to a linear scale and to take the count in meters or kilometers. In Fig. 3 the measured distance is 1070 m.
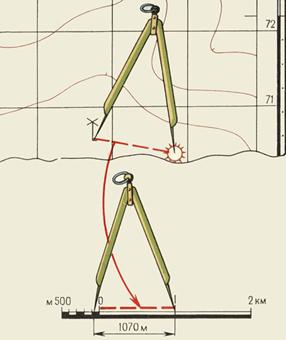 Fig. 3. Measurement on a map of distances by a circular meter on a linear scale. |
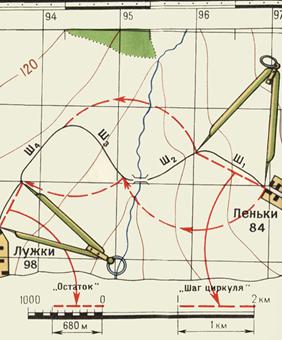 Fig. 4. Measurement on the map of distances by a measuring instrument on winding lines. |
Large distances between points along straight lines are usually measured using a long ruler or a circular meter.
In the first case, to determine the distance from the map using the ruler, use the numerical scale (see Figure 2).
In the second case, the "step" solution of the meter circulator is set so that it corresponds to an integer number of kilometers, and a whole number of "steps" is plotted on the segment measured on the map. The distance that does not fit into the whole number of "steps" of the measuring circle is determined with the help of a linear scale and added to the obtained number of kilometers.
The distances along the sinuous lines are measured in the same way (Fig. 4). In this case, the "step" of the measuring instrument should be taken as 0.5 or 1 cm, depending on the length and degree of tortuosity of the line being measured.
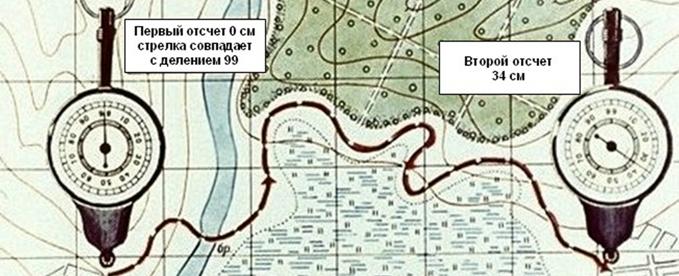
Fig. 5. Measurement of distance by a curvimeter
To determine the length of the route on the map, a special device is used, called the curvimeter (Figure 5), which is especially useful for measuring tortuous and long lines.
The device has a wheel, which is connected by a transmission system with an arrow.
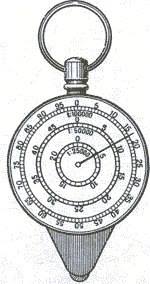
When measuring the distance with the curvimeter, you need to set its arrow on division 99. Holding the curvimeter in a vertical position leads it along the measured line, without taking it from the map along the route so that the scale readings increase. Having brought to the end point, count the measured distance and multiply it by the denominator of numerical scale. (In this example, 34x25000 = 850000, or 8500 m).
Accuracy of measuring distances on the map. Corrections for the distance for incline and tortuosity of lines
The accuracy of determining the distances on the map depends on the scale of the map, the nature of the measured lines (straight, meandering), the chosen method of measurement, the terrain and other factors. The most accurate way to determine the distance on the map is in a straight line.
When measuring distances with a circular meter or a ruler with millimetric divisions, the average error of measurement in flat areas of the terrain usually does not exceed 0.7-1 mm on the scale of the map, which is for a scale of 1: 25000 - 17.5-25 m, Scale 1: 50000 - 35-50 m, scale 1: 100000 - 70-100 m.
In mountainous areas, with a steep slope, the errors will be greater. This is due to the fact that when surveying a terrain, the map is not drawn with the length of the lines on the surface of the Earth, but with the length of the projections of these lines on the plane.
For example, With a steep slope of 20 ° (Figure 6) and a distance of 2120 m, its projection to the plane (distance on the map) is 2000 m, ie, 120 m less. It is estimated that at a slope angle (steepness of the slope) of 20 °, the result of measuring the distance along the map should be increased by 6% (at 6 m), at an angle of 30 ° - by 15%, and at an angle of 40 ° - by 23 %.
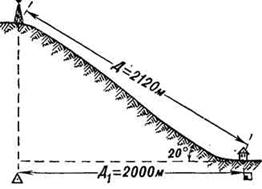
Fig. 6. Projection of the length of the slope to the plane (map)
When determining the length of the route on the map, it should be borne in mind that the distances along the roads measured on the map using a compass or a curvimeter are in most cases shorter than the actual distances.
This is due not only to the presence of descents and ascents on the roads, but also to some generalization of the road gyrations on the maps. Therefore, the result of the route length measurement obtained on the map should be multiplied by the factor indicated in the table taking into account the nature of the terrain and the scale of the map.
| The simplest methods of measuring areas on a map | |||
|---|---|---|---|
Nature of the area |
The coefficient of increasing the length of a route measured on a scale map |
||
1: 50000 |
1: 100,000 |
1: 200,000 |
|
Mountain (strongly crossed) |
1.15 |
1.20 |
1.25 |
Hilly (mid-intersected) |
1.05 |
1.10 |
1.15 |
Plain (slightly intersected) |
1.00 |
1.00 |
1.05 |
An approximate estimate of the size of the areas is made by eye by the squares of the kilometer grid that is on the map. Each square of the grid of maps of scales 1: 10000 - 1: 50000 on the terrain corresponds to 1 km2, the square grid of maps of scale 1: 100000 - 4 km2, the square grid of maps of scale 1: 200000 - 16 km2.
More precisely, the areas are measured by a pallet, which is a sheet of transparent plastic with a grid of squares with a side of 10 mm applied to it (depending on the scale of the map and the required accuracy of the measurements).
By placing such a pallet on the measured object on the map, first calculate the number of squares completely within the object's contour, and then the number of squares of the object crossed by the contour. Each of the incomplete squares is taken as half the square. As a result of multiplying the area of one square by the sum of squares, the area of the object is obtained.
On squares of scales 1: 25000 and 1: 50000 of the area of small sections it is convenient to measure an officer's ruler, which has special notches of rectangular shape. The areas of these rectangles {in hectares) are indicated on the ruler for each scale of the plot.
Determination of distances along rectangular coordinates
The distance D along a straight line between points with known rectangular coordinates given in one system can be determined most accurately by the formula:
D=V(Х2-Х1)2+(Y2-Y1)2 Where:
- X1, Y1 - coordinates of the starting point;
- X2, Y2 - coordinates of the end point.


Comments
When commenting on, remember that the content and tone of your message can hurt the feelings of real people, show respect and tolerance to your interlocutors even if you do not share their opinion, your behavior in the conditions of freedom of expression and anonymity provided by the Internet, changes Not only virtual, but also the real world. All comments are hidden from the index, spam is controlled.