Start of section
Production, amateur
Radio amateurs
Aircraft model, rocket-model
Useful, entertaining 		Stealth Master
Electronics
Physics
Technologies
Inventions 		Secrets of the cosmos
Secrets of the Earth
Secrets of the Ocean
Tricks
Map of section
Start
Forum
Use of the site materials is allowed subject to the link (for websites - hyperlinks)

Navigation: =>

Home / Physics / Discoveries /

Physical processes are considered in the formation, propagation, interference, and diffraction of acoustic waves

TO THE QUESTION OF WAVE INTERFERENCE

INTERFERENCE OF ACOUSTIC WAVES. DIFFRACTION. EDUCATION OF ACOUSTIC WAVES

Stetsovich VI

Leave a comment

Physical processes are considered in the formation, propagation, interference, and diffraction of acoustic waves.

It is shown that the energy density that is transported by a wave is proportional to the amplitude and frequency of the oscillations of the source, and with the interference of the waves, the energy of the resulting oscillation is equal to the sum of the energies of the emerging waves.

Modern wave theory explains a very wide range of observed in nature wave processes. And, nevertheless, the analysis of interference effects leads to results that contradict the conclusions of the wave theory.
In accordance with generally accepted concepts, when two coherent waves propagating in one direction are added at a certain observation point:

Will again be a harmonic oscillation of the same period:

Amplitude A and initial phase The resulting oscillation is determined from the vector diagram ( Figure 1 ):

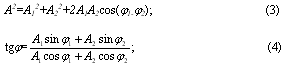
Since the energy density of the wave is proportional to the square of the amplitude of what oscillates, the energy of the resultant vibration is not equal to the sum of the energies of the emerging waves and varies from interference to interference At At the point of the interference maximum up to At At the points of the interference minimum.
In the simplest case, the amplitudes of the interfering waves are equal: , The amplitude of the resulting oscillation changes from zero at a minimum to 2A at the maximum, and the corresponding intensities from 0 to 4A 2 .

The damping of oscillations in some places and their amplification in others are not connected with any transformations of the energy of oscillations. Thus, with interference, the matter reduces, as it were, only to a redistribution of the vibrational energy and a change in the direction of its transfer, but the law of conservation of energy is strictly fulfilled [1].

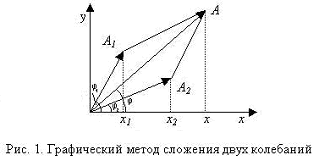
INTERFERENCE OF ACOUSTIC WAVES. DIFFRACTION. EDUCATION OF ACOUSTIC WAVES

The distribution of the energy density of the sound wave along the direction of its propagation is shown in Fig . 2 [2]. It can be seen from the figure that, in the region of condensation and in the rarefaction region, equal energy flows are transferred by the wave, so when interference of two waves occurs, and at the point of the interference maximum (ie, A , Fig. 3 ), when the amplitudes of pressures and velocities add up, and At the point of the interference minimum (ie, O , Fig. 3 ), when a region of condensation of one wave is superimposed with the region of rarefaction of the other, two sections of waves are superimposed which carry the same energy, which must be equally fixed by the instruments. Nevertheless, energy is not fixed at the points of the interference minimum.

The redistribution of energy to the points of the interference maximum is possible only if the direction of energy transfer by the wave changes with interference. Considering in this case a larger path and a constant velocity of propagation of the wave energy in the medium, it would be possible to record a slowdown in the propagation of wave energy in the interference region. Since this is not observed, it should be assumed that in the interference region, the energy is transported by the wave at a rate greater than the velocity of propagation of the wave in the medium, which is obviously unrealistic.

When the wave propagates, one passes through the other, completely without affecting one another. In the same way, when passing points with zero amplitude of oscillations during interference (ie, O , Fig. 3 ), the two coherent waves encountered propagate further without any changes and at the maximum point (ie, A , Fig. 3 ), summation of the wave amplitude is observed without any Either temporary delays. Consequently, the waves carry energy through the points of the interference minimum and there is no redistribution of energy to the points of the interference maximum.
Problems also arise when explaining the interference of electromagnetic waves. The electromagnetic wave is a collection of variables of electric and magnetic fields propagating in space and, since, when two coherent waves are superimposed, the electric field strength is zero continuously at the point of the interference minimum, the propagation of the wave further without variable fields ( E and H ) through the interference minimum point is impossible . It is also unclear why, after passing the interference minimum, the amplitude of the electromagnetic wave increases.

In the case of a corpuscular interpre- tation of the phenomenon of interference of electromagnetic waves, it is impossible to explain how the energy maximum is observed at the point of the interference maximum, which exceeds the sum of the energies of the incoming photons, and it is completely incomprehensible how and where the energy and momentum transferred by the photons vanishes at the point of the interference minimum They arise after its passage.

The essence of the wave process is the transfer of energy from one point of space to another, etc. What is the mechanism of energy transfer through areas of space, where measurements show the absence of waves and, accordingly, the transfer of energy?

INTERFERENCE OF ACOUSTIC WAVES. DIFFRACTION. EDUCATION OF ACOUSTIC WAVES

To explain these phenomena, it seems necessary to consider in more detail the processes that occur when waves arise and propagate. Since the basic laws of wave motion are the same, we will consider the case, which is most simply explained visually - the propagation of a sound wave in an ideal gas.

In analyzing the processes that occur when a sound wave propagates in an ideal gas, we assume that:

  • The gas molecules have the same mass;
  • When collisions of molecules with each other - the interaction is elastic, according to the laws of collision of balls;
  • Two molecules are encountered as a result of the motion; Simultaneous collisions of three or more molecules are unlikely;
  • Particles experience only frontal collisions that lead only to a change in the direction of the colliding molecules and do not change the direction of their velocities to some other angles;
  • Molecules can move in the direction of the coordinate axes x, y, z , and out of 1/3 of the total number of molecules moving along the x axis , half moves in the direction of the screen, which will be a source of disturbances, and the other half of it;

INTERFERENCE OF ACOUSTIC WAVES. DIFFRACTION. EDUCATION OF ACOUSTIC WAVES

Let the screen move with velocity u in the direction of the x- axis under the action of an external force ( Fig . 4 ). An arbitrarily chosen gas molecule moving toward the screen at a speed of " -u0 " after the impact will have a velocity u0 + u . In this case, the fact that the temperature of the medium and the screen are the same is taken into account, and during the interaction the molecule first adsorbs on the surface of the screen and after a while flies away, having a screen velocity u0 relative to the screen, and relative to the external observer u0 + u . If we consider the process of interaction of a molecule with a moving screen as an elastic impact of balls, then the velocity of the molecule will be u0 + 2u, and all the formulas given below will differ only in the coefficients.

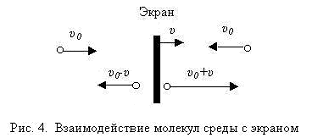
In any case, the momentum and kinetic energy of the molecules increase, which leads to an increase, in comparison with the unperturbed state, of the internal energy of the gas.

On the opposite side of the screen, after collision with it, the velocity of the molecules will decrease: u0 -u , and the internal energy of the gas will be less than the initial, unperturbed state.

The resulting perturbation of the physical parameters in the medium, as a result of the interaction between the particles in accordance with the conservation of momentum of the closed system, will propagate at a speed c , moving from the screen, half of the particles moving along the x axis, carries the perturbation energy, and after collision with particles moving Towards the opposite direction, the energy corresponding to the energy of the particle in the unperturbed state of the medium ( Fig. 5a, b ).

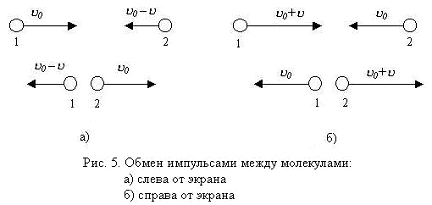
When the screen moves, the density of particles also changes.

Bearing in mind that u «c , in the region of condensation to the right of the screen [3]:

In this case, the kinetic energy of the particles in a unit volume, which transport the energy of the disturbance in the direction from the screen, is equal to:

And the kinetic energy transferred at the same time by the other half of the particles in the opposite direction to the screen:

The difference between (7) and (8) determines the magnitude and direction of the energy disturbance carried by the wave and to the right of the screen, where the condensation pulse propagates, the energy density of the wave is equal to:

By analogous calculations, we find the energy density, which is carried by the rarefaction wave to the left of the screen:

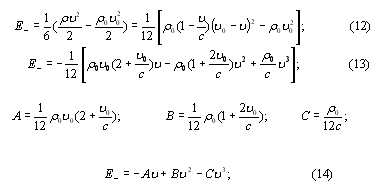
As the wave propagates, the concentration of particles of the medium changes; The average distance between them, so the potential energy of the allocated volume of the medium also changes. In the classical theory, the wave energy consists of the kinetic energy of the vibrating particles of the medium and the potential energy of the elastic deformation of the medium, and the densities of the kinetic and potential energies are equal at any instant of time and at any point in the medium ( Fig . 2 ).
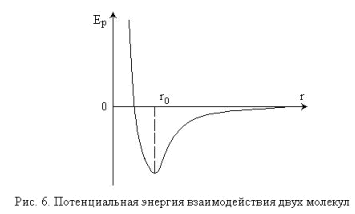
The potential energy of interaction of two particles as a function of the distance between them has approximately the form shown in Fig . Under normal conditions ( p = 1 atm and T = 200С, r ~ 10r0 ), the distance between the air molecules r » r0 , therefore, when the sound wave propagates in such a medium, the potential energy of the medium in the rarefaction region increases, and in the condensation region (in contrast to Classical theory) is reduced. Taking into account, however, the fact that for gas molecules under given conditions Ek> Ep , the change in the potential energy of the interaction of molecules, in the propagation of acoustic waves in the atmosphere, can practically be neglected in comparison with the change in their kinetic energy, and the gas can be regarded as ideal.

The rate of oscillation of the screen u «c and u« u0 . Then, neglecting in (10) and (13) terms proportional to u2 and u3 , we can fairly well assume that in the general case, in vector form, the energy density carried by a plane wave:

Where the vector u determines the value of the wave energy and the direction of its propagation.
If the oscillations of the screen are harmonic: x = Xsinwt and its velocity u = Xw coswt , then the value of the energy density transferred by the wave is fundamentally different from the energy values ​​determined by the classical formulas [ 4, p.363 ]: the wave energy is proportional to the density of the medium, the velocity of the chaotic thermal The motion of molecules, the amplitude and frequency, and not the squares of the amplitude and frequency of oscillations of the source.

The energy components proportional to u2 and u3 make an appreciable contribution to the wave energy values ​​at large amplitudes and oscillation frequencies of the source that, when propagating, for example, acoustic waves in a medium, leads to nonlinear effects.

The momentum acquired by the particles in a unit volume of the medium during the propagation of the condensation wave is:

Since the direction of the screen velocity u every half-period varies, then every half-period (in contrast to the classical theory) the direction of the momentum and energy carried by the wave changes. The instantaneous distribution of internal energy in the medium and the direction of energy transfer during the propagation of a plane wave along the x axis at some point in time are shown in Fig . 7 , where E is the direction of energy transfer by the wave emitted by the source, and Es is the direction of energy transfer due to Redistribution of the internal energy of the medium (the screen is placed at the origin). The instantaneous energy of the transported wave E (x, t) at the point x at time t (Fig. 8) is equal to:

Moreover, a positive value of E means that the direction of energy and wave propagation coincide, the negative value - the energy is transferred (in contrast to the classical theory) in the opposite direction.

In practice, when recording an acoustic wave and its parameters, the sound pressure is determined, and as a receiver for acoustic vibrations, microphones are used that somehow follow the fluctuations in the pressure of the medium during the passage of the wave and transform them into electrical oscillations, and in classical physics the wave intensity is proportional to the square of the sound pressure .
It is known that the gas pressure in an unperturbed medium:

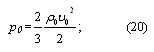
In this case, the change in the pressure of the medium on the membrane of the microphone during the propagation of the sound wave caused by the change in particle density and velocity is determined from the expression:

Noting that the value in parentheses is proportional to the energy transferred by the wave, we come to the conclusion that the energy density of the wave, and, accordingly, the sound intensity, is proportional to the amplitude of the sound pressure, and not to its square:

The reason for all these differences is that in the classical theory, when calculating the wave energy, the fact that the particles of the medium already have an initial velocity and kinetic energy before the appearance of a perturbation in the medium is ignored ( Fig. 7 ).

The principle of the interference of waves is fundamentally different from the generally accepted one.

In the classical version, if two coherent waves are excited in a homogeneous and isotropic medium, then at any point in space, waves are superimposed in accordance with the principle of superposition: each point (molecule) of the medium to which two or more waves arrive, simultaneously takes part in the oscillations caused by Each wave separately [2]. To determine the motion of a particle, the motion of a particle of the medium in each wave is found separately, and then these movements are summed up ( Fig . 1 ).

In this variant: two particles, each of which carries a disturbance caused by two different sources of oscillations, exchange impulses in the case of interaction: the first after the collision will transfer the impulse transferred to it by the second particle until the next collision and vice versa: the second particle will transfer the momentum transferred to it First, i.e. Each particle takes part in the transfer of the disturbance from only one source ( Fig . 5 ). The variant of interaction shown in Fig . 1 is possible only in the case of simultaneous impact of two particles in the third, but, according to the initial conditions, such an event is unlikely. Therefore, for particles of a medium in which several waves propagate, the principle of superposition is unacceptable: each particle participates in the transfer of momentum and energy from only one source, or: a perturbation from different sources is carried by different particles.

Because of this, it can be asserted that, with interference, the waves propagate, without affecting one another, the redistribution of energy flows and other interactions as a result of superposition of waves, and the total energy density at the observation point is equal to the total energy density of the interfering waves:

If two waves with the same amplitudes propagate in the same direction, the amplitude of the sound pressure doubles at the points of the interference maximum, and, therefore, the energy densities of the folding waves are summed up ( Fig . 9a ). At points of the interference minimum, when the region of condensation of one wave is superimposed with the region of rarefaction of the other, the signal is not fixed, since in this case the directions of energy and momentum transfer by the interfering waves are opposite, and, for equal amplitudes of oscillations, their total action on the microphone membrane is zero ( Fig. .9b ). Therefore, when waves are added, one must take into account not only the magnitude of the energy and momentum transferred by the wave, but also the direction of their transfer.

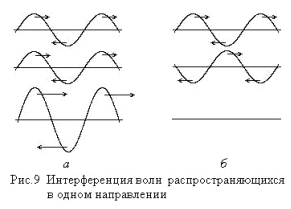
Similar processes occur in a standing wave.

It is known that when two coherent, equal amplitudes, running in opposite directions, interfere, the resulting wave motion is called a standing wave. A standing wave is characterized by the presence of nodal points (the points of the interference minimum) whose amplitude of oscillations is zero, the particles of the medium do not move at all at these points, according to the classical concepts, there is no energy transfer and, in general, the energy does not propagate along the standing wave, only Particles between nodes oscillate and exchange energy [2].

In this interpretation, the explanation is different.

In the so-called. Nodal points of the particle, moving continuously, in one direction carry the energy of a wave running in the same direction before colliding with particles that carry the energy of a wave propagating in the opposite direction. After collision and exchange of pulses in the opposite direction until the next collision, the particles carry a pulse of a wave propagating in the same direction. Thus, periodically changing the direction of motion and exchanging impulses, the particles alternately transfer the energy of both waves, so they propagate each in their direction without affecting one another. With the help of receivers of sound waves, for example, microphones, at small oscillation amplitudes, counterflows of energy and momentum through the nodal points of the standing wave and the points of interference minimum with interference of waves with equal amplitudes of oscillations can not be detected, since their action on the receiver is the same in magnitude, but Opposite in direction and as a result is zero. But, nevertheless, at the points of the interference minimum, the waves do not "quench" each other, and the state of the "excited" particles at the nodal points: velocity, energy, and particle density, differs from the corresponding quantities in the unperturbed medium.

So far, when considering the propagation of waves, the fact that collisions of particles lead to a change in the direction of the velocity of the colliding particles to some angles different from the initial direction of wave propagation was not taken into account. As a result of these deviations, the energy of the wave transported by the particles can propagate at an angle to the original direction. According to the area of ​​the screen (source of waves), these energy flows (due to the randomness of the processes of motion and scattering of molecules in collisions) will on the average be mutually compensated, and only on the lateral boundaries of the plane wave will propagation of wave energy away from the original direction. Analogous processes will also occur when a wave meets an obstacle, which is the cause of the diffraction of waves.

Similar processes of transmission or diffusion of the amplitude of oscillations along the wave front (across the beam) are also observed when the wave propagates when the amplitude along the wave front changes.

The wave carries momentum and energy from one place of space to another, while it is believed that all particles of the medium involved in the transfer of energy, all the time fluctuate around the equilibrium position. It can be seen from (10), (13) and (16), (17) that, in the propagation of a longitudinal wave, the momentum and energy transferred to the positive half-wave exceed the transferred momentum and energy in the negative half-wave by the values, respectively:

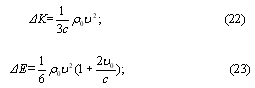
Which leads to the transfer of the substance of the medium by a sound wave, and at high amplitudes it leads to the appearance of a constant flux in the form of a so-called Acoustic currents.

CONCLUSIONS

  1. The energy carried by the wave is proportional to the amplitude and frequency of the oscillations of the source, and not to their squares.

  2. With interference, the energy of the resulting oscillation is equal to the sum of the energies of the folding waves.

  3. The energy carried by the perturbation wave is characterized not only by the magnitude, but also by the direction of its transfer, and when the harmonic wave propagates in the medium, the direction of the transfer changes every half-way.

LITERATURE

  1. G.S. Landsberg, Optics, Science, Moscow, (1976), p. 88.

  2. S.P. Strelkov, Mechanics, Science, Moscow, (1975), p. 481.

  3. S.E. Haykіn, Фізичні основи механіки, Radianska School, Kyiv, (1966), с.674.

  4. VE Kuzmichev, Laws and formulas of physics, Naukova Dumka, Kiev, (1989), p. 363.

print version
Authors: Stetsovich VI
Date of publication 10.11.2006гг