Start of section Production, amateur Radio amateurs Aircraft model, rocket-model Useful, entertaining	Stealth Master Electronics Physics Technologies Inventions	Secrets of the cosmos Secrets of the Earth Secrets of the Ocean Tricks Map of section
Use of the site materials is allowed subject to the link (for websites - hyperlinks)

BALL LIGHTNING

Welcome to the forum

Let's start with some assumptions. First, ball lightning exists without energy from outside, i. E. Energy is only needed at the initial moment. After formation (for example, as a result of an electric discharge), ball lightning exists without absorption of additional energy. Secondly, the ball lightning consists of a plasma, i.e. From a fully ionized substance.

How does the formation of ball lightning. Suppose that due to the supply of a large amount of energy (for example, with a powerful electric discharge), in a certain volume a plasma of Fig. 1. a.

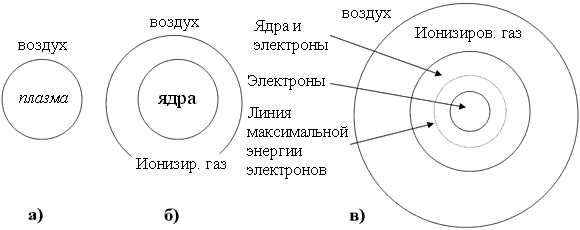
Fig. 1. The sequence of formation of ball lightning.

At the same energy, the velocity of the electrons is much greater, the speed of the nuclei. Electrons first leave the volume of the plasma, ionizing on their way some volume of ambient air. As a result, at this stage an internal, positively charged region is formed, consisting of nuclei and surrounding this region, the ionized gas of Fig. 1.b. The free electrons of the ionized gas are accelerated into the interior of the positively charged region, reaching maximum energy in its center. As a result, we get the picture shown in Fig. 1.c. Due to the expansion of the nuclei, an area with a very small concentration of nuclei is formed in the center. We assume that only electrons are in this region. With such a charge distribution, we have: the central negative charge slows the electrons moving from the region of the ionized gas, and therefore the maximum of the electron energy will be located not in the center of the ball lightning but on the sphere indicated in Fig. 1. in the dotted line. The same central charge slows down the nuclei that fly away from the center of the ball lightning. Atoms of air can not interfere with these processes. Their velocities are much less than the velocities above the particles considered, and the process of formation of ball lightning has time to end before the air atoms pass any significant distance. Later, there is an increase in the negative charge in the center, which is already capable of slowing down and accelerating the positive nuclei when moving toward the center. After a while, an equilibrium state sets in, which we shall consider. Let us take such a model of ball lightning.

Fig. 2. Section of ball lightning

In Fig. 2 shows a section of ball lightning. The motion of the nuclei and electrons that make up ball lightning is an oscillatory motion under the action of an electric field. All the kernels, i. Practically the entire mass of the ball lightning, are inside the brown sphere with points B 1 and B. In the volume bounded by the red and brown lines, the energy of the nuclei is zero. When moving toward the center of ball lightning, the nuclei are accelerated, acquiring the maximum energy in the center. Moving from the center, they slow down to zero energy in the interval between points A and B. Such a motion of positively charged nuclei is due to a central negative charge. Now consider the motion of electrons. They have the maximum energy on the sphere with point B , and the zero energy at the center of the ball lightning between the blue and blue lines (lines with points C and D ), i.e. Electrons are accelerated from point D to point B , and then slow down as they move toward the center of the ball lightning. After this, they again accelerate to point B and slow down when they move to point D. Let us consider the charge distribution over the radius of ball lightning. This distribution is shown in Fig. 3.

Fig. 3. Distribution of charge along the radius of ball lightning.

How is this distribution of the charge obtained? The particles at different points along the radius of the ball lightning have different energies, and hence different velocities. The more the velocity of a particle in a certain region, the shorter the time it is in this region and the smaller charge is concentrated in a given volume. Conversely, the smaller the energy of particles in some volume, the greater the charge is concentrated in this place. The electron energy is minimal at the center of the ball lightning and in the interval between the points C and D , and the energy of the nuclei in the interval between the points A and B. This means that in these places the negative and positive charges are concentrated. This is shown in Fig. 3. The positive charge in the region of point E is due to other causes, which are discussed below. These charges create an electric field inside the ball lightning. The distribution of the potential and the strength of this field are shown in Fig. 4 and Fig. 5.

Fig. 4. Distribution of the potential of the electric field f along the radius of the ball lightning

Fig. 5. Distribution of electric field strength along the radius of ball lightning

Of all the above graphs, you can draw some conclusions. In the center there is a negative charge, which, although less than two times, of a positive charge with a maximum on the sphere with point A , nevertheless creates an increase in the potential of the electric field from the center of the ball lightning to point B , and if the maximum energy of the nucleus is divided by the charge The nucleus is smaller than the potential difference between the points O and B , then such a nucleus can not penetrate beyond point B and leave the ball lightning limits.

To illustrate this statement, consider the problem. We have a central negative charge at the point O and a positive charge twice the size of the sphere distributed around the sphere with center O. As a result, the resultant Coulomb force, directed to the center of the sphere, will act on the trial, positive charge placed on the surface of the sphere. The influence of the central negative charge will be greater than the effect of the positive charge distributed over the sphere. Thus, the central charge holds around itself positively charged nuclei. On the other hand, the total charge inside the sphere with point B will be positive. And already this positive charge does not give electrons (because they are negatively charged) to fly beyond point E and leave the ball lightning.

Now let us consider the question of how ball lightning particles interact with the air atoms surrounding it. On the periphery of the ball lightning are only electrons and the closer they are to the boundary, the less their energy. The main interaction with the gas atoms occurs in the region where the electron energy is close to the thermal energy. The process of interaction of air atoms with electrons of ball lightning is shown schematically in Fig. 6.

Fig. 6. Interaction of electrons of ball lightning with atoms of air

Atoms of air interact with the counterflow of electrons. In the blue region of Fig. 6 the electron energy is approximately equal to the thermal energy and the interaction with the atoms will be elastic, since The energy of the electron is not enough for the excitation of the electron shells, and even more so for the ionization of the atom. At the same time, it suffices to communicate the momentum of the reverse direction to the atom. It should be noted here that a change in the direction of motion of particles in the central potential field does not lead to a decrease in the mean oscillation energy. There is a possibility that the atom will pass this region, hitting the orange region with a higher electron energy (this probability depends on the electron flux density). In this case, the atom is ionized, the electron becomes a ball lightning, and the ion is pushed out by an electric field beyond its limits. As a result, we find that inside the sphere with point D in Fig. 2 ball lightning is charged negatively. The ions will accumulate on the sphere with point E in Fig. 2 . This is the point where the effect of a positively charged volume inside the sphere with point B in Fig. 2 and affects the total negative charge of ball lightning, i.e. These ions can be considered a part of ball lightning. With this positive charge, ball lightning will be electrically neutral.

As a result of this interaction, electrons lose a small part of the energy, because This interaction occurs in the region of low electron energies. On the other hand, the loss of energy by electrons, reduces the radius of ball lightning. This leads to a decrease in the surface of the ball lightning and to an increase in the electron flux density through it, which in turn reduces the probability of penetration of air atoms into the region of high-energy electrons. Thus, ball lightning always tries to come to an equilibrium state.

Now consider how this model is consistent with the described observers, the behavior of ball lightning in natural conditions.

The glow of ball lightning, the smell of ozone can easily be explained by the penetration of atoms and air molecules into the region of high electron energies. Because of this, ionization or excitation of the electron shells of atoms occurs, the destruction of chemical bonds.

If conditions are created and ball lightning has lost stability (for example, collision with a solid object), then an instantaneous release of energy concentrated in the ball lightning occurs. This can be regarded as an explosion. If, however, ball lightning lose all energy gradually, it will look as if it "melted" in the air.

Fig. 7. Interaction of ball lightning with solid objects

We consider Fig. 7 , which shows the interaction of ball lightning with solid objects. If during this interaction the ball lightning does not lose stability, then that part of the solid object (in figure 7 is denoted by a thick line), which falls into the region of high electron energies, will be ionized. In this case, ball lightning will partially lose energy. So, flying along a tree, ball lightning can leave burns on it. Thin objects (leaves, rag, tent), it can burn through.

Since the charges are not uniformly distributed over the radius of the ball lightning, its motion in space can be influenced by the external electric field of Fig. 8 . Different density of lines of electric field strength creates a force acting on ball lightning.

Fig. 8. Influence of the external electric field of ball lightning on its motion in space.

In the end, we will dwell on some points. The proposed model of ball lightning is based only on the Coulomb interaction of charged particles. Initially, the divided charges form a vibrational system where each charged particle moves under the action of an electric field, and the totality of all particles creates this field. In the interaction of particles with air atoms, there is no significant loss of energy; This interaction occurs in the region of low electron energy. At the center of ball lightning, the nuclei have a maximum energy and, possibly, it is greater than the threshold energy of thermonuclear reactions. This means that if you create a ball lightning from thermonuclear materials (T, D or He ³ ), then it is possible to obtain energy.

print version
PS The material is protected.
Date of publication 26.09.2003gg

NEW ARTICLES AND PUBLICATIONS
	The technology of manufacturing universal couplings for unbreakable, threadless, flossless connection of pipe sections in high pressure pipelines (video is available )
	Technology of oil and oil products cleaning
	On the possibility of moving a closed mechanical system at the expense of internal forces
	Fluorescence in thin dielectric channels
	The relationship between quantum and classical mechanics
	Millimeter waves in medicine. A New Look. MMV therapy
	Magnetic engine
	Heat source based on pump units