home Other disciplines books Ically mathematical programuvannya - Nakonechny S.І.

Ically mathematical programuvannya - Nakonechny S.І.

3.4. Butt zastosuvannya teorії dvoїstostі for znahodzhennya optimally planіv pryamoї that dvoїstoї tasks

Cutaneous s dvoh conjugation problem can be rozv'yazati okremo against vstanovlenі theorems dvoїstostі zalezhnostі mіzh optimal plan pryamoї that dvoїstoї tasks umozhlivlyuyut znahodzhennya rozv'yazku dvoїstoї zadachі for nayavnostі optimal plan pryamoї, i navpaki.

Before zadanoї zadachі lіnіynogo programuvannya zapisati dvoїstu task. Rozv'yazati one h them the simplex method is the optimal plan viznachiti Druha zadachі, vikoristovuyuchi spіvvіdnoshennya pershoї dvoїstostі theorem.

max Z = - 5 2 x1 + x2;

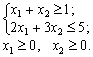
Rozv'yazannya. Perche nіzh zapisati dvoїstu task neobhіdno direct problem zvesti to standard viglyadu. Oskіlki tsіlova funktsіya maksimіzuєtsya F i in sistemі obmezhen Je nerіvnostі then їh slіd zvesti to mean " 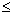". Tom Pershe obmezhennya zadachі pomnozhimo (-1). Pіslya tsogo sign nerіvnostі zmіnitsya on protilezhny. Otrimaєmo:

max Z = - 5 2 x1 + x2;

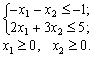
Teper for vіdpovіdnimi rules sklademo dvoїstu problem:

min F = - y1 + 5 y2;

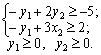
Oskіlki zapisanі zadachі simetrichnі, then whether they can yak s rozv'yazati simplex method. Napriklad, viznachimo spochatku optimally pryamoї zadachі plan. For tsogo zastosuєmo algorithm simplex method.

1. max Z = - 5 2 x1 + x2 + x3 + 0 0 x4;

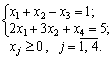
2. The vector form recording system obmezhen Got viglyad:

.

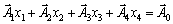de . . . . .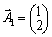

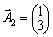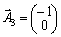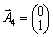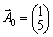In sistemі vektorіv for utvorennya Pochatkova odinichnogo basis vіdsutnіy one vector. Tom vvedemo boxed zmіnnu in Pershe obmezhennya.

3. Rozshirena task lіnіynogo programuvannya bude with such a:

max Z = - 5 2 x1 + x2 + x3 + 0 0 x4 - x5 M;

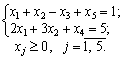
In tsіy zadachі x 4 x 5 that - bazisnі zmіnnі, and x1, x2, x3 - vіlnі. Nekhay x1 = x2 = x3 = 0, todі x4 = 5; x5 = 1.

Purshia zadachі support program:

X = 0 (0, 0, 0, 5, 1), Z 0 = - M.

4. Away rozv'yazuvannya pryamoї zadachі filed in viglyadі simpleksnoї tablitsі:

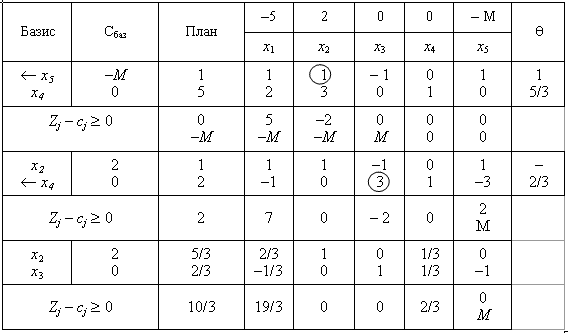
W ostannoї simplex tablitsі zapishemo optimal plan pryamoї zadachі:

X * = (0; 5.3; 2.3; 0), Z max = 10/3.

Zgіdno Zi spіvvіdnoshennyam dvoїstostі for Perche theorem can visnovuvati scho optimal plan dvoїstoї zadachі іsnuє i

min F = max Z = 10/3.

Components of the vectors Y * (optimally dvoїstoї zadachі plan) viznachimo of the formula:

.

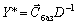de 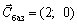that mіstitsya in stovpchiku "sbaz" ostannoї simplex tablitsі;

.

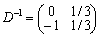Matrix D- 1 takozh mіstitsya in ostannіy simplex tablitsі in stovpchikah zmіnnih «x5» that «x4», SSMSC utvoryuvali Pochatkova basis.

Otzhe,

.

min F = - 0 1 x + 5 x 2/3 = 10/3.

Zastosuvavshi for rozv'yazuvannya pryamoї zadachі simplex method, mi znayshli її optimal plan and potіm viznachili optimally rozv'yazok dvoїstoї zadachі for Relief spіvvіdnoshen pershoї dvoїstostі theorem.

Before zadanoї zadachі lіnіynogo programuvannya zapisati dvoїstu task. Rozv'yazavshi dvoїstu task grafіchno, viznachiti optimal plan pryamoї zadachі.

min Z = x1 + x2 + 2 2 x3;

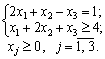
Rozv'yazannya. For vіdpovіdnimi rules pobuduєmo dvoїstu problem:

max F = y1 + 4 y2;

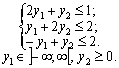
Zauvazhimo scho zadachі nesimetrichnі, i y1 to zmіnna scho Persha vіdpovіdaє rіvnyannyu in sistemі obmezhen pryamoї zadachі, mother Mauger whether yaky sign and zmіnna v2 - nevіd'єmna deprivation.

Dvoїsta task Got Dvi zmіnnі and otzhe, її mozhna rozv'yazati grafіchno (Fig. 3.2).

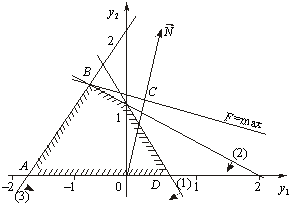
Fig. 3.2

Naybіlshogo values tsіlova funktsіya dvoїstoї zadachі F dosyagaє in tochtsі In bagatokutnika ABCD. Її coordinates viznachimo rozv'yazannyam Sistemi rіvnyan:

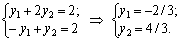
Otzhe, Y * = (- 2/3; 4/3); max F = 1 x (- 2/3) + 4 x 4/3 = 14/3.

Optimal plan pryamoї zadachі viznachimo for Relief spіvvіdnoshen Druha dvoїstostі theorem.

Pіdstavimo Y * in system obmezhen dvoїstoї zadachі i z'yasuєmo, yak vikonuyutsya obmezhennya tsієї zadachі:

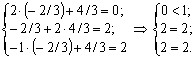
Oskіlki Pershe obmezhennya for optimal plan dvoїstoї zadachі vikonuєtsya yak strict nerіvnіst then visnovuєmo scho Persha zmіnna pryamoї zadachі dorіvnyuvatime zero x 1 = 0 (Persha Chastina Druha dvoїstostі theorem).

Teper proanalіzuєmo optimally dvoїstoї zadachі plan. Oskіlki other component v2 = 4/3 dodatna plan, the other obmezhennya pryamoї zadachі for X * vikonuvatimetsya yak strictly rіvnyannya (other Chastina Druha dvoїstostі theorem).

Ob'єdnuyuchi zdobutu іnformatsіyu can zapisati system obmezhen pryamoї zadachі yak dvoh rіvnyan system in yakіy x1 = 0, that viznachiti Rasht zmіnnih:

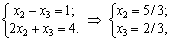
tobto = X * (0; 5/3; 2/3), min Z = 0 + 1 x 2 x 2 x 5/3 + 2/3 = 14/3.

Umov min Z = max F = 14/3 vikonuєtsya, i that X * = (0, 5/3, 2/3); Y * = (- 2/3; 4/3 ) Je optimal plan vіdpovіdno pryamoї that dvoїstoї tasks.

Viznachiti, chi Je optimally takі Plagne sformulovanoї zadachі lіnіynogo programuvannya:

12 min Z = x1 - x2 + 2 4 x3;

a) X = (8/7, 3/7, 0); b) X = (0; 5.1; 8.5); c) X = (1/3, 0, 1/3).

Rozv'yazannya. Principle rozv'yazuvannya problems of this type ґruntuєtsya on vikoristannі Druha dvoїstostі theorem. Neobhіdno pobuduvati dvoїstu task one dopuskayuchi scho vіdpovіdny plan x ∈ optimally viznachiti optimally rozv'yazok dvoїstoї zadachі. Yakscho at tsomu ekstremalnі values ​​tsіlovih funktsіy will odnakovimi for value, then stewed properly. Protilezhne mozhna visnovuvati such vipadkah:

1. Yakscho zaproponovany plan X is unacceptable, not tobto zadovolnyaє system obmezhen pryamoї zadachі.

2. Yakscho viznacheny dvoїstoї plan zadachі unacceptable, tobto not zadovolnyaє OAO All obmezhennya dvoїstoї zadachі.

3. Yakscho viznacheny plan dvoїstoї zadachі admissibility, ale for Demba ekstremalne values tsіlovoї funktsії F does not dorіvnyuє funktsії the Z values, tobto not vikonuєtsya Umov pershoї dvoїstostі theorem.

Zapishemo dvoїstu task to pryamoї zadachі lіnіynogo programuvannya:

max F = y1 + 2 y2;

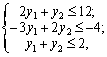
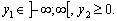
Perevіrimo zaproponovanі Plagne on optimalnіst.

1. X = (8/7, 3/7, 0). Pіdstavimo yogo in obmezhen pryamoї zadachі:

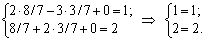
Obidva obmezhennya vikonuyutsya, i to X = (8/7, 3/7, 0) Je feasible plan pryamoї zadachі. Pripustimo Teper scho zaznacheny plan Je optimal plan pryamoї zadachі. Todі rozrahuєmo for Demba value tsіlovoї funktsії: Z = 12 x 8/7 - 4 3/7 x 2 + x 0 = 12.

Skoristaєmosya other theorems that dvoїstostі viznachimo vіdpovіdny dvoїstoї zadachі plan. Oskіlki x1 = 8/7> 0; x2 = 3/7> 0, then by another zgіdno s Chastain Druha theorem dvoїstostі mozhna zapisati Pershe that other obmezhennya rіvnyannya yak i viznachiti y1 that v2:

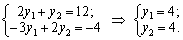
Pіdstavimo tsі value in tretє obmezhennya Sistemi dvoїstoї zadachі:

;

.

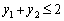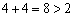For viznachenih values y1 = 4; v2 = 4 tse obmezhennya not vikonuєtsya, i plan to vіdpovіdny y = (4; 4) Je inadmissibility up dvoїstoї zadachі. Vnaslіdok tsogo our assumptions, scho X = (8/7, 3/7, 0) Je optimal plan pryamoї zadachі, viyavilosya pomilkovim.

2. X = (0; 5.1; 5.8). Pіdstavimo Tsey plan in obmezhen system pryamoї zadachі:

Feasible plan, i for Demba Z = 12 x 0 - 4 x 1/5 + 2 x 8/5 = 12/5.

Viznachimo vіdpovіdny plan dvoїstoї zadachі. Oskіlki components that x 2 x 3 dodatnі, others i tretє obmezhennya dvoїstoї zadachі mozhna zapisati yak rіvnyannya:

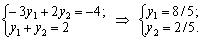
Perevіrimo, chi vikonuєtsya Pershe obmezhennya dvoїstoї zadachі for viznachenih values y1 that v2: 2 x 8/5 + 2/5 = 18/5 <12 Otzhe, Pershe obmezhennya vikonuєtsya, i to v = (8/5, 2/5) Je feasible plan dvoїstoї zadachі. For Demba

F = 8/5 + 2 x 2/5 = 12/5 = Z.

W look around to vikladene mozhna visnovuvati scho Y * = (8/5; 2/5) Je optimal plan dvoїstoї zadachі and X * = (0; 1/5; 8/5) - optimal plan pryamoї zadachі.

Our stewed vіdnosno zaproponovanogo plan viyavilosya correctly.

3. X = (1/3, 0, 1/3). For tsogo plan obmezhennya pryamoї zadachі vikonuyutsya as follows:

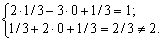
Oskіlki X = (1/3, 0, 1/3) Je inadmissibility of the plan, the vіn not Mauger Buti takozh optimal plan pryamoї zadachі.

Otzhe, perevіrka zaproponovanih planіv on optimalnіst gave takі result of: a) ni; b) so that X = (0; 1/5; 8/5), min Z = 12/5; c) ni.