home Other disciplines Books Mathematics programmers - Nakonechny S.I.

Mathematics programmers - Nakonechny S.I.

3.5.1. Analis to the range of the component of the vector of the

It is permissible, but to the action k-that the omegenya ( 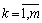) Має в правій частині початкове значення - 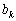. Nekhay Potchkova value was changed by the amount 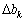. Otzhe, k- that in the system (3.37) budey mati viglyad:

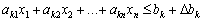. (3.39)

For zvedennya (3.39) before the canonical type neobhidno enter dodatkovu zmіnnu xn + k (yakschoo obesezhenya moe viglyad rivnyannya, then yak taku zmіnnu mozhna rozglyadati nevіd'єmnu piece zmіnnu).

A. Roshglanemo vipadok, if dodatkov zmіnna in the optimal plan neazisna i dorivnjue zero.

The first theorems of the two-fold approach, the optimal plan for direct tasks (yak i kozhen pochnichnyi oboronniy plan), can be taxed in the following way:

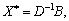(3.40)

De D is the matrix, and the vector component 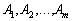The remaining basis; 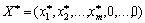- the optimal plan of problems (3.36) - (3.38); B is a vector that is stored in the oldest terms in the rest of the simplex table.

The annulus, which is a component of the vector B , is replaced by 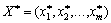. However, I do not have a band, 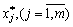Zalishayutsya nevіd'єmnimi, tobto structure of the optimal plan does not zminyuetsya. Viznachimo tsі interii.

Vector 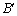Подамо у вигляді:

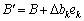, (3.41)

De ek is a single-vector stochvpik, and in it's odinitsya - k- th component. Todi, vikoristovoychi (3.40), маємо:

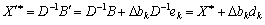, (3.42)

Dek dk - (the dot matrix of the matrix D-1 into the single vector ek ) is the k- th matrix of the matrix D-1.

Significantly, the k- th stovpchika matrix 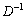across 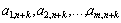, Тоді:

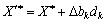Abo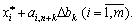

Ostanja is a simplex table with mothers wigs:

Table 3.3

Oskilki neobhidno, shob plan 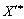Takozh buv optimalnym, mia vikonuvatisya umova nevіd'єmnosti all components of the given vector, annealing,

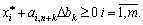(3.43)

Звідси:

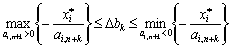. (3.44)

Тоді нижньою та верхньоюBorders зміни значення bk will be advised to:

;

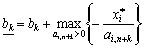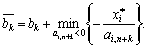
Yaksho not існує жодного 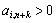for 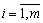, Then 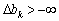, But not one thing 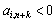for 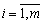, Then .

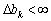For problems, the knowledge of the minimum value of the function and that of the system type " 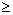»Meaning Δ bk змінює знак, оскільки замість нерівності 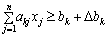It is possible to raise a rarity of nerves .

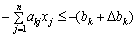Separator, for 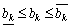For being of any value , Що відповідає додатковій необзисній змінній 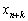, The structure of the optimal task plan, (3.36) - (3.38), be filled with post.

In . Roshglanemo vipadok, if dodatkov zmіnna - is basic.

(3.42) dk is the single-vector vector with the kth component, the same frequency, the annulus, and the system of nerves (3.43) is transformed into taku:

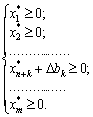
Obviously , the value of an add-on basis is determined by the range of factors, in which the component bk can be interchanged (zbilshuvatys for obmezhen type " ").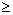

The optimal plan is to fill up the uneven in the range bk + Δ bk for silent 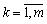, Yakim vidpodayayut dobatkovі basis zmіnnі xn + k , de

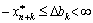(3.45)

For interchanging systems (3.37) with the type " ".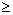

For problems, the knowledge of the minimum value of the function and the interchange of systems (3.37) with the type " 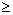»Mozhilі zmіni component of the legal parti sistemi obmenen viznachayutsya z nervіvnosti:

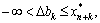De, 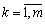. (3.46)

C. Yaksho components of the vector of the old members in the systems of interchange of tasks of linear programming to change the water hour for a number of chi all the values 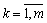, Then the boundary of the possible values ​​of the quantities 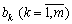It is a folding problem. However, in such a conversation, you can pereviriti, chi zadovolnyayut concrete zmіni values 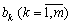System view:

,

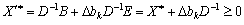De is an identity matrix. Якщо позначити елементи матриці 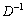across 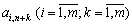, Тоді:

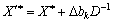Abo .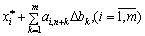

Oskilki neobhidno, shob plan 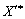Takozh buv is optimal, maє vikonuvatisya ura nevіd'єmnosti vseh components of the vector, annealing:

,

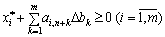Toto:

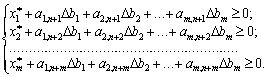(3.47)

Якщо значення 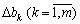(3.47), then the structure of the optimal task plan (3.36) - (3.38) is filled with post.

For viznachennya top of the lower border zmіn 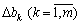, In the interstices of which the structure of the optimal plan is to be filled with a post, it is necessary to isolate the system of nerves (3.47). One of the best practices for the knowledge of the optimal plan for the new tasks of linear programming 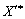Simplify the problem in a simplex method, zmіneyuchi vіlnі devcheny sistemi (3.37) on .

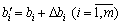D. For two persons the value 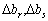, That is, to satisfy the system (3.47), to the prichom for the optimal plan for the alternation, and to recom- mend 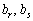, The system (3.37) yikon yak rivnyannya, mozhna viznachiti norm zamistchennya, sho show, naskilki neobhidno zbilshiti (zmenshiti) value 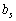For zmenshennia (zbilshennia) 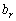, But the meaning of the tsil'ovoy function was lapped with an indescribable nemism.

In the third theorem, two-sidedness, but for small values 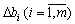, Tobto for such a value increase, yakі not zmіniyut znachennya dvuhistih otsіnok, and ozhe, zadovolnyayut system (3.47), Vikonuetsya rivnyannya: 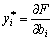, Abo

.

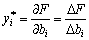Do not change the value of br to Δ br . Viznachimo, yak neobhіdno zmіniti bs , shchob znachennja tsil'ovoy funkії shrouded himself. Зміна br means, що 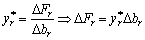, Analogous to zmіni 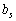on 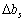Маємо: 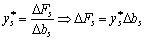. Abi znachenny funktsionala zalishalsya nezminnim, neobhidno, shob

.

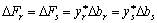Звідси виразимо шукания вплив 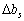on :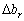

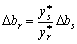. (3.48)

At the time the values ​​of the values ​​of br br b b znachenny tsil'ovoy funktsii tasks (3.36) - (3.38) do not zminitsya, proto optimalnogo plan budesh. Nehai problem (3.36) - (3.38) describes the vyznachennya optimal vibrokhnitsva plan for the minds of the resource mismanagement.

The economical volume of the pressures (3.44), (3.45), (3.46), (3.47) is in this way, vio vyny vyznachayut borders and zaginnyh osyagіv resursiv, in the interstices of which is indicated the optimal plan for the structure of viribnitsa products to be filled with ungain.

Рівняння (3.48) viznachaєe, kaklyu kіlkіstyu one resource mozhna zamіniti іnshy resurs, shchob tsіlова functіія не змінилась, причому розглядаються лише ті resources, які використаі поністю at виробництві production for the best plan.