home
 Other disciplines Other disciplines
 Books Books
 Mathematics programmers - Nakonechny S.I. Mathematics programmers - Nakonechny S.I.
|
Mathematics programmers - Nakonechny S.I.
8.4.2. The Lagrange multiplication method
Іode to the method of the set of Lagrange polygases in the vice-pochatkoy problems and simple. For ts'go tsil'ovu funktsiyu zamenyuyut іnshoyu, з більшою кількістю змінних, тобто такою, яка вклює в себе уми, що подані як обмеження. Pislya such peredvorennya further rozv'yazuvannya zadachi polagaє in znahodzhennі екстремуму нової functції, on змінні anchors are not imparted nyakih обмежень. Tobto vіd pochatkoyї problemy poshuku umnogo ekstremumu pereodimo to problemi vidushkanya ozumnovnogo ekstremalnogo znachennosti ihnshoi funktsii. Otzhe, zavdyaki such peretvorennu mozhlive zastosuvannya methodіv klassicnogo znachodzhennja ekstremumu funktsії kіlokh zmіnnih.
In the next paragraph, the need is imposed for the establishment of a local, non-permissive and differential function of two zmins.
Узагальнення необхідної момоіінунуняня local екстремуму functції n змінних має аналогічний вигляд. Otzhe, for rozv'yazuvannya zadachi neobhіdno znayti viraz partnikh pohhіdnih noviy tsil'ovoy funktsii z kozhnyi zmіnnoyu i pririvnyati їh to zero. As a result, otrimaemo system rivnyan. Її rozv'yaz viznachaє so zvanі statsіonarnyі dots, sered yakih і і шукані екстремальні значення функції.
Rozglyanemo the method of Lagrange multipliers for rozvjazuvannya tasks and nonlinear programming, but moe viglyad:
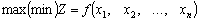 (8.6)
(8.6)
For the mind:
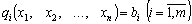 , (8.7)
, (8.7)
De functions 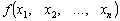 I
I 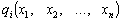 Мають бути диференційовними.
Мають бути диференційовними.
The problem (8.6), (8.7) is a field in the well-known extremal function 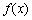 For the brains of the vimeana
For the brains of the vimeana 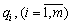 .
.
Moved to the task of a crazy crazy ekstremumu. In the literature [13, 28] it is theoretically brought to the conclusion that the formulation of such problems is exclusive.
Замінюємо цільову функцію (8.6) on the fold. Tsya functitsіya nazivayutsya functіією Лагража і має такий вигляд:
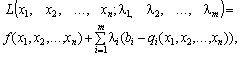 (8.8)
(8.8)
De 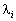 - Acts of nevidomi magnitudes, but nazivayutsya multipliers of Lagrange.
- Acts of nevidomi magnitudes, but nazivayutsya multipliers of Lagrange.
Significantly, partial, and priivnyaemo їх to zero:
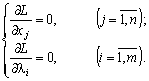
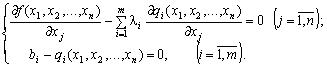 (8.9)
(8.9)
Friend grupa рівнянь системи (8.9) забезпечує виконання умов (8.7) початкової tasks нелінійного програмування.
The system (8.9), as a rule, is not linear.
Розв'язками її є 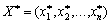 I
I 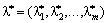 - stationary points. Оскільки, ці розв'язки отримані з необхідноїї умоіextremum, then you can not maximize, minimize tasks (8.6), (8.7) can not be joined to points of the transect (with dots).
- stationary points. Оскільки, ці розв'язки отримані з необхідноїї умоіextremum, then you can not maximize, minimize tasks (8.6), (8.7) can not be joined to points of the transect (with dots).
For dinogostuvannya statsionarnih points and viznachennya type ekstremumu neobhidno pereviriti vikonannya suficient minds ekstremumu, tobto dosloditi in okolі statsionarnih points of differentiation to another order (yakshcho for funktsiy 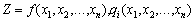 Існують другі частинні похідні і вони неперервні).
Існують другі частинні похідні і вони неперервні).
Uzagalennnja dostatnogo umovi іsnuvannya local ekstremumu for funktsii n zmіnnih lead up to such a rule: for the Lagrange function, the form (8.8) will be the matrix of Hesse, which is the block structure of rozmyrnistyu 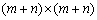 :
:
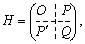
De O - matrix rozmirnistyu 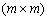 , Scho warehousing z zulovikh elemementov,
, Scho warehousing z zulovikh elemementov,
P - matrices for rozmyrnistyu 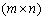 , The elements are supposed to be:
, The elements are supposed to be:
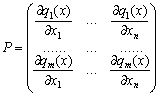 ,
,
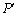 - the matrix is transposed to P rozmіrnistyu
- the matrix is transposed to P rozmіrnistyu 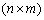 ,
,
Q - matrix of rozmyrnistyu 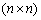 Mind:
Mind:
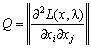 , De
, De 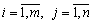 .
.
Rozglyanemo know the form of extinction systems (8.9). Nehaj statsionnaya dot moe coordinate 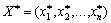 I
I 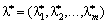 .
.
1. Point  Точ the maximum point, yakzcho, starting with the head minor the order ( m + 1), the onset ( n - m ) of the head minions in the matrix, the familiar numeric series, the sign of the first term, which is to be multiplied by the multiplier
Точ the maximum point, yakzcho, starting with the head minor the order ( m + 1), the onset ( n - m ) of the head minions in the matrix, the familiar numeric series, the sign of the first term, which is to be multiplied by the multiplier 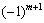 .
.
2. Point 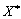 Є the point of the minimum, yakshcho, starting with the head minor the order ( m + 1), the sign of the oncoming ( n - m ) head minions in the matrix is to be multiplied
Є the point of the minimum, yakshcho, starting with the head minor the order ( m + 1), the sign of the oncoming ( n - m ) head minions in the matrix is to be multiplied 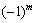 .
.
The problem is rozglyanemo, rozvjazok zakogo znaydemo a method mnogozhiv Lagrange.
 Акціонерне fellowship with obedeleniyu vidpodalnistyu seen 1,200 hectares of the pіd of the basic sіl'skogoospodarsky culture - winter wheat and tsukrovі Buryaks.
Акціонерне fellowship with obedeleniyu vidpodalnistyu seen 1,200 hectares of the pіd of the basic sіl'skogoospodarsky culture - winter wheat and tsukrovі Buryaks.
In Table. 8.1 маємо техніко-економічні показники вирощування цих crops:
Table 8.1
Pokaznik |
Ozyma wheaten x 1, honeycomb |
Цукрові буряки х 2, сотні га |
Yield, t / ha |
4 |
35 |
Price, UAH / t |
800 |
300 |
Ownership, UAH / t |
|
|
It is necessary to know the optimum area for winter wheat and tsuchiki buryakiv.
Nekhay: x 1 - palli pіd під winter wheat, сотні га;
X 2 - area of the piww piq tsukroviami buryakami, sotni ha.
Zvernemo respect for those, scho sobivartist tone of wheat and tsuchikih Buryakiv zalizhit vіd vіdpіdіnosti ploschі sіvu.
The economics and mathematics model is written down. Criterion optimality vizmemo maksimizatsiu net income:
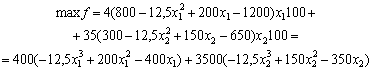
For the mind:
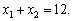
We write down the Lagrange function:
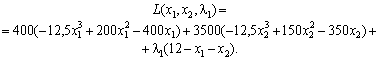
Візьмемо частинні похідні і прирівняємо їх to zero:
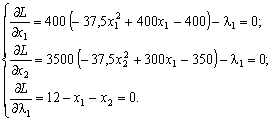
З цієї системи рівнянь визначаємо координати сідлових точкаок. The first one of the other is known l1 і, pririvnejuchi virazy, maєmo:
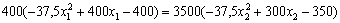 (8.10)
(8.10)
Abo, skorotivshi on 100 obydvіі partini and rozkrivshi arches, otrimaemo:
 . (8.11)
. (8.11)
Із останнього рівняння системи маємо:  .
.
Pisstavmo visaz for 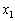 At the level of (8.11). Отримаємо:
At the level of (8.11). Отримаємо:
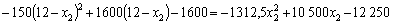
Abo
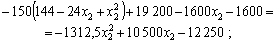
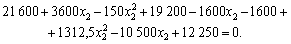
The oil, 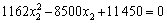 ;
;
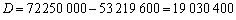
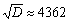 .
.
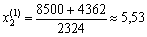 (553 ha);
(553 ha);
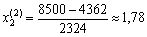 (178 hectares).
(178 hectares).
Відповідно дістаємо:
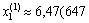 Ha);
Ha);
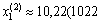 Ha).
Ha).
Tobto otrimali dvі sіdlovі points:
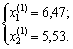
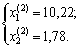
Perevimimo for dopomogo dostatnyo umovi іsnuvannya ekstremumu spotchatka sidlovu point 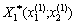 .
.
The matrix of Hesse is such a visage:
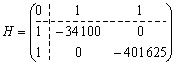 .
.
For vischezaznachenim rule of viznachaemo golovni miori, pochinayuchi z second order ( 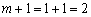 ):
):
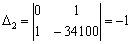 ,
,
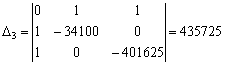 .
.
Otzhe, golovnі мінори utloryuyut znakomizіnnyi number ta, poichinauchi z nichnogo mnoru 2 nd order, oncoming mnor viznachaetsya sign 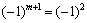 , Tobto
, Tobto 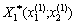 Є point to the maximum.
Є point to the maximum.
The value of the value of the function in the calculation is computed:

Analogical calculation for points 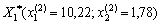 Pokazuyut, scho vona not єextreme.
Pokazuyut, scho vona not єextreme.
Otzhe, tsil'ova funktsiya nabuda znachennoy znachennya, yakshcho ozima wheat viroshchuvatimetsya on the area of 647 hectares, and tsukrovi Buryaks - on a surface of 553 hectares.
The method of Lagrange multipliers can be zastosovuvatysya takozh y raz nayavnosti obmezhen on signs zmіnnih i obmezhen-nervijnostej.
Rozglyanemo taku task in the foul vizglody:
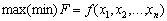 ,
,
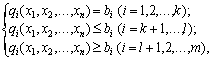
Prichomu vse functiki, scho enter the task, mute bouti difentsitsiovnimi hocha b once.
Obviously, it is introduced in the partial part of the system by interchanging the tasks of the non-addictive non-predecessors 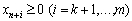 Peretvoruyet pochatkovu task in taku, sho mistit lishe obmezhennia-rivnosti, tobto yaka for the mold and the method of rozv'yazuvannya zbiagitimsya z zadachiu (8.6), (8.7). The problem of the origin of this type of problem is outlined in the literature: [19], [28] ].
Peretvoruyet pochatkovu task in taku, sho mistit lishe obmezhennia-rivnosti, tobto yaka for the mold and the method of rozv'yazuvannya zbiagitimsya z zadachiu (8.6), (8.7). The problem of the origin of this type of problem is outlined in the literature: [19], [28] ].

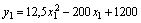


Comments
Commenting on, remember that the content and tone of your message can hurt the feelings of real people, show respect and tolerance to your interlocutors even if you do not share their opinion, your behavior in the conditions of freedom of expression and anonymity provided by the Internet, changes Not only virtual, but also the real world. All comments are hidden from the index, spam is controlled.