home Other disciplines books Ically mathematical programuvannya - Nakonechny S.І.

Ically mathematical programuvannya - Nakonechny S.І.

8.6. Kuhn-Tucker theorem

Rozglyanuty method mnozhnikіv Lagrange umozhlivlyuє znahodzhennya deprivation locally sіdlovih tochok funktsії Lagrange.

Kuhn-Tucker theorem daє zmogu vstanoviti tipi tasks for yakih on mnozhinі admissibility rozv'yazkіv іsnuє deprivation one global ekstremum zumovlenogo type. Vaughn tіsno pov'yazana s neobhіdnimi that dostatnіmi minds іsnuvannya sіdlovoї point.

Rozglyanemo task nelіnіynogo programuvannya, yak, do not zmenshuyuchi zagalnostі, will file in viglyadі:

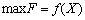(8.22)

(8.23)

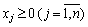. (8.24)

(Obviously, scho sign nerіvnostі mozhna zmіniti on protilezhny breeding lіvoї i pravoї Chastain obmezhennya at (- 1)).

Theorem 8.1. (Kuhn-Tucker theorem). The vector X * Je optimally rozv'yazkom zadachі (8.22) - (8.24) todі i tіlki todі, if іsnuє Taqiy vector 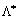Scho at 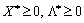for vsіh 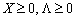dot 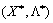Je sіdlovoyu funktsії Lagrange point

.

i funktsіya methylene 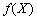for vsіh 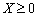ugnuta and funktsії 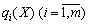- Opuklі.

BROUGHT. Neobhіdnіst. Nekhay X * - optimal plan zadachі (8.22) - (8.24), Je tobto points of global maximum zadachі. Otzhe for vsіh іnshih planіv zadachі X s mnozhini admissibility rozv'yazkіv vikonuvatimetsya spіvvіdnoshennya:

.

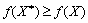Now the vector Rozglyanemo 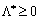Scho vіdpovіdaє tochtsі global maximum 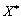, I values ​​funktsії Lagrange points . . de 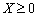- Dovіlny plan zadachі s mnozhini admissibility rozv'yazkіv, - Vector mnozhnikіv Lagrange, scho vіdpovіdaє X.

W Minds (8.21) maєmo: , todі

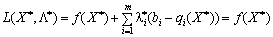. (8.25)

For a point z coordinates deyakі dodanki mind mozhut Buti vіdmіnnimi od zero. Oskіlki of minds zadachі 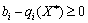, The deprivation of minds, scho 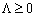, Matimemo nerіvnіst:

.

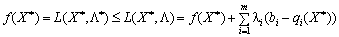Funktsіya 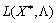- Lіnіyna vіdnosno 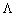, Tobto Stop nerіvnіst vikonuєtsya to whether yakogo . Otzhe, point 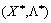- A point on the global mіnіmumu funktsії Lagrange.

For vstanovlennya nerіvnostі scho vіdpovіdaє lіvіy chastinі Minds (8.13), and the Same: 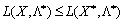, Skoristaєmosya takozh rіvnyannyam (8.21), pіdsumuvavshi Yogo for i: 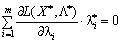. Over the minds of the theorem 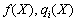- Ugnutі funktsії i 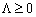, To vikonuєtsya TAKE rіvnyannya:

Otzhe have tochtsі X * funktsіya Lagrange Got the global maximum of the X, scho povnіstyu bring neobhіdnіst theorem.

Dostatnіst. To bring the minds dostatnostі theorem potrіbno vihoditi s of scho . 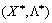- Sіdlova point funktsії 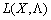(For tobto 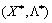vikonuєtsya nerіvnіst (8.13)), i neobhіdno bring, scho todі X * Je optimal plan zadachі opuklogo programuvannya.

Pіdstavimo in nerіvnіst (8.13) viraz funktsії Lagrangian (8.12) for zadachі (8.22) - (8.23):

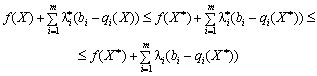(8.26)

when vsіh values .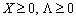

Rozglyanemo law Chastain podvіynoї nerіvnostі (8.26).

.

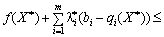
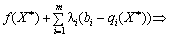
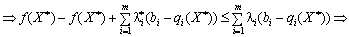
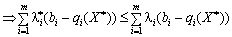Stop nerіvnіst Got vikonuvatisya for vsіh 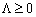. Krіm order 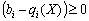, Tobto nerіvnіst spravdzhuєtsya deprivation in razі, if

.

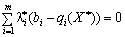Todі s lіvoї Chastain nerіvnostі (8.26) maєmo:

.

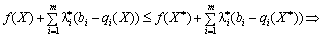
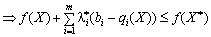Through those scho 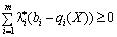, Prihodimo to nerіvnostі 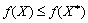, Yak spravdzhuєtsya for vsіh values .

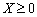Otzhe, point X * zadovolnyaє obmezhennya i nadaє maximum value tsіlovіy funktsії zadachі, the fact scho for vsіh іnshih funktsіya 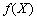nabuvaє Mensch value nіzh tochtsі in X *, tobto Won Je optimal plan zadachі nelіnіynogo programuvannya. Terem minds Dostatnіst brought.

Minds theorem of Kuhn - Tucker vikonuyutsya deprivation for tasks scho mіstyat opuklі funktsії.