- Цветы и растения
- Аквариум и рыбы
- Для работы
- Для сайта
- Для обучения
- Почтовые индексы Украины
- Всяко-разно
- Электронные библиотеки
- Реестры Украины
- Старинные книги о пивоварении
- Словарь старославянских слов
- Все романы Пелевина
- 50 книг для детей
- Стругацкие, сочинения в 33 томах
- Записи Леонардо да Винчи
- Биология поведения человека
Главная  Экономика Экономика  Книги Книги  Моделювання економіки - Вітлінський В.В. Моделювання економіки - Вітлінський В.В. |
Моделювання економіки - Вітлінський В.В.
РОЗДІЛ 8. МОДЕЛІ ПОВЕДІНКИ ВИРОБНИКІВ
Максимізація прибутку — основний критерій, на який орієнтуються виробники. Але це не єдиний критерій. Максимізація поточного прибутку повинна співвідноситися зі стратегічним прогнозом розвитку фірми тощо.
8.1. Модель фірми
Нехай виробнича фірма випускає один продукт (чи багато продуктів, але з постійною структурою). Річний випуск у натурально-речовій формі X — це кількість одиниць продукту одного виду (чи кількість багатономенклатурних агрегатів).
Використані ресурси: L — жива праця (у вигляді середньої чисельності зайнятих за рік чи відпрацьованих за рік людино-годин); K — засоби праці (основні виробничі фонди); M — предмети праці (витрачене за рік паливо, енергія, сировина, матеріали, комплектувальні вироби тощо).
Кожен з агрегованих видів ресурсів (праця, фонди, матеріали) має певну кількість різновидів.
Позначимо вектор-стовпчик можливих обсягів витрат різних видів ресурсів через x = (x1, …, xn)?. Тоді технологія фірми визначатиметься її виробничою функцією, яка виражає зв’язок між витратами ресурсів і випуском:
X = F(x). (8.1)
Припускається гіпотеза, що F(x) двічі неперервно диференційована і неокласична, до того ж матриця її других похідних є від’ємно визначеною.
Якщо w = (w1, …, wj, …, wn) — вектор-рядок цін ресурсів, а р — ціна продукції, то кожному вектору витрат х відповідає прибуток:
П(х) = pF(x) – wx. (8.2)
У (8.2) R = pX = pF(x) — вартість річного випуску фірми або її річний дохід, C = wx — витрати виробництва чи вартість витрат ресурсів за рік.
Якщо не вводити інших обмежень, окрім невід’ємних витрат ресурсів, то задача на максимум прибутку набере вигляду:
 (8.3)
(8.3)
Це задача нелінійного програмування з n умовами невід’ємності x ? 0, необхідними умовами її розв’язання є умови Куна—Таккера:

 (8.4)
(8.4)
Якщо в оптимальному розв’язку використовуються всі види ресурсів, тобто x* > 0, то умови (8.4) матимуть вигляд:
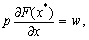 (8.5)
(8.5)
або
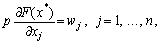
тобто в оптимальній точці вартість граничного продукту даного ресурсу повинна дорівнювати його ціні.
Такий самий (за формою) розв’язок має задача на максимум випуску за заданого обсягу витрат
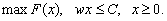 (8.6)
(8.6)
Це задача нелінійного програмування з одним лінійним обмеженням і умовою невід’ємності змінних.
Побудуймо функцію Лагранжа:
L(x, l) = F(x) + l (C – wx),
тепер максимізуємо її за умови невід’ємності змінних.
Для цього необхідно, щоб виконувались умови Куна—Теккера:
 (8.7)
(8.7)
Як бачимо, умови (8.7) цілком збігаються з (8.4), якщо покласти 
Приклад Випуск однопродуктової фірми задається виробничою функцією Кобба—Дугласа:
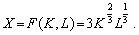
Визначимо максимальний випуск, якщо на оренду фондів і оплату праці виділено 150 грош. од., вартість оренди одиниці фондів wk = 5 грош. од., ставка зарплати wL = 10 грош. од./люд.
Якою буде гранична норма заміни одного зайнятого фондами в оптимальній точці?
Розв’язання. Оскільки F(0, L) = L(K,0) = 0, то в оптимальному розв’язку K* > 0, L* > 0, тому умови (8.7) наберуть вигляду:
 (8.8)
(8.8)
або у нашому випадку:
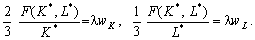
Поділивши перше рівняння на друге, маємо:
 .
.
Підставивши цей вираз в умову:

знайдемо

Розв’язання можна проілюструвати геометрично. На рис. 8.1 зображені ізокости (лінії постійних витрат для С = 50, 100, 150) та ізокванти (лінії постійних випусків для Х = 25,2; 37,8).
Ізокости мають такі рівняння:
5K + 10L = C = const.
Ізокванти —


Рис. 8.1. Ізокости постійних витрат та ізокванти постійних випусків
В оптимальній точці K* = 20, L* = 5 ізокванта X* = 37,8 та ізокоста С = 150, що проходять через цю точку, дотикаються, бо згідно з (8.8) нормалі до цих кривих, задані градієнтами 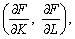
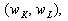 колінеарні.
колінеарні.
Норма заміщення праці фондами в оптимальній точці:
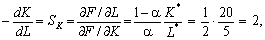
тобто один працюючий може бути замінений двома одиницями фондів.
Розв’язуючи задачу моделі фірми (8.3) на максимум прибутку, знаходимо єдиний оптимальний набір ресурсів x* > 0 (розглядається випадок, коли всі ресурси входять до набору). Цьому набору відповідає єдине значення витрат: C* = wx*.
Розв’язуємо задачу моделі фірми (8.6) на максимум прибутку за заданих витрат С*. Якщо F(x) — неокласична, то в оптимальному розв’язку  причому цей розв’язок єдиний.
причому цей розв’язок єдиний.
Таким чином, з одного боку,
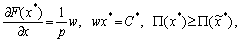
а з іншого —

Оскільки

то
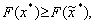 але
але 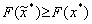 , тому
, тому 
Через те що розв’язок задачі (8.3) єдиний, то 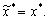
Отже, якщо задача на максимальний прибуток має єдиний розв’язок x* > 0, то їй відповідає задача на максимальний випуск за заданих витрат С* = wx*, причому остання має такий самий розв’язок, як і перша (див. рис. 8.1): 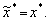
Геометричне місце точок дотику ізокост та ізоквант за різних значень витрат C визначає довготерміновий шлях розвитку фірми X(C), тобто показує, як зростатиме (спадатиме) випуск, якщо витрати зростуть (зменшаться). Оскільки ця залежність монотонна, то існує обернена монотонна функція витрат С = С(Х).
Оскільки Х(С) — максимальний випуск за заданих витрат С, то витрати С(Х), які відповідають цьому максимальному випуску Х, — мінімальні, а оптимальний обсяг випуску знову ж визначається за умови максимального прибутку:
 . (8.9)
. (8.9)
Прирівнюючи до нуля похідну
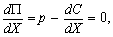
бачимо, що в оптимальній точці граничні витрати дорівнюють ціні випуску:

Окрім того, максимум прибутку досягається за
 (бо
(бо  ).
).
Розгляньмо n співвідношень (8.5):
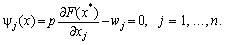
Ці співвідношення можуть бути розв’язані відносно х в околі оптимальної точки х*, якщо якобіан  де
де

Це означає, що повинен бути відмінним від нуля гессіан  виробничої функції (але H від’ємно визначений, тому дійсно
виробничої функції (але H від’ємно визначений, тому дійсно 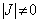 ), тоді
), тоді
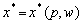 (8.10)
(8.10)
або
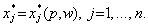
Ці n рівнянь задають функцію попиту (на ресурси), відшукані за допомогою моделі поведінки фірми. Функції попиту на ресурси можна також знайти експериментально за допомогою методів математичної статистики за відповідними вибірковими даними.
Функція пропозиції —
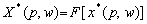 .
.
Подібно до рівняння Слуцького, що показує реакцію споживача на зміни цін товарів, аналогічні рівняння описують реакцію виробника на зміну цін випуску і ресурсів.
За умови заданих цін p, w поведінка виробника визначається таким співвідношенням (усього (n + 1) співвідношень):
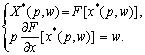 (8.11)
(8.11)
Нехай тепер ціна випуску змінилася чи змінилася ціна ресурсів, або і те і те.
1. Реакція виробника на зміну ціни випуску.
Диференціюємо (8.11) за р:


або в матричному позначенні:

де  — вектор-рядок,
— вектор-рядок, 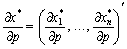 — вектор-стовпчик, або
— вектор-стовпчик, або
 (8.12)
(8.12)
Рівняння (8.12) являє собою реакцію виробника (зміну випуску) (зміну попиту на ресурси) на зміну ціни випуску р.
2. Реакція виробника на зміну цін ресурсів.
Нехай змінилася ціна k-го ресурсу wk, тоді диференціюємо рівняння (8.11) за wk:
 (8.13)
(8.13)
Якщо позначити
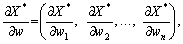
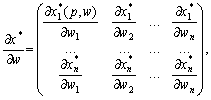
то n(n + 1) рівняння (8.13) у матричній формі запишуться таким чином (це реакція виробника на зміну цін ресурсів):
 (8.14)
(8.14)
3. Реакція виробника на одночасну зміну ціни випуску та ціни ресурсів. Поєднання (8.12) та (8.14) дає основне матричне рівняння теорії фірми:
 (8.15)
(8.15)
яке показує реакцію виробника на одночасну зміну ціни випуску і цін ресурсів.
Розв’язуючи (8.15) відносно зміни випуску  і зміни попиту на ресурси
і зміни попиту на ресурси 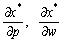 , отримуємо:
, отримуємо:
 (8.16)
(8.16)
Скориставшись правилом обернення блочних матриць, маємо:
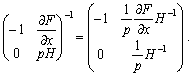
Підставляючи останній вираз у (8.16), отримаємо систему рівнянь фірми відносно змін випуску і попиту на ресурси:
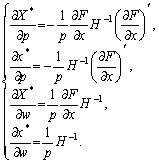 . (8.17)
. (8.17)
Перше рівняння системи (8.17) показує, як зміниться випуск за зростання ціни на продукцію фірми. Оскільки матриця Гессе H від’ємно визначена, то H –1 — також, тому
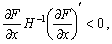
отже,
 (8.18)
(8.18)
тобто зі зростанням ціни випуску обсяг випуску продукції зростає.
Таким чином,  ,
,
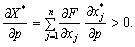 (8.19)
(8.19)
Але 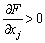 (для неокласичної функції граничні продукти додатні), тому обов’язково деякі
(для неокласичної функції граничні продукти додатні), тому обов’язково деякі 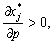 тобто зростання ціни випуску приведе до зростання попиту на деякі ресурси.
тобто зростання ціни випуску приведе до зростання попиту на деякі ресурси.
Ресурс l-го виду називають малоцінним, якщо 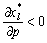 з (8.17) видно (друга та третя група рівнянь), що
з (8.17) видно (друга та третя група рівнянь), що  або у розгорнутому вигляді —
або у розгорнутому вигляді —
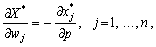 (8.20)
(8.20)
тому зростання ціни на продукцію зумовлюватиме підвищення (зниження) попиту на окремі види витрат, якщо підвищення ціни на цей вид ресурсів приводить до скорочення (зростання) обсягів оптимального випуску. Зокрема, збільшення ціни на малоцінний ресурс сприятиме збільшенню випуску.
Підставляючи (8.20) у (8.19), отримаємо
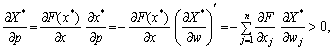
тому з 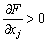 випливає, що
випливає, що 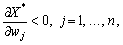 тобто зростання ціни на деякий вид ресурсів зумовить скорочення випуску.
тобто зростання ціни на деякий вид ресурсів зумовить скорочення випуску.
Згідно з (8.17)

тому матриця 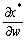 — від’ємно визначена, отже,
— від’ємно визначена, отже, 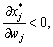 тобто підвищення ціни на деякий ресурс завжди призводить до спаду попиту на нього, отже, криві попиту є спадними.
тобто підвищення ціни на деякий ресурс завжди призводить до спаду попиту на нього, отже, криві попиту є спадними.
Оскільки матриця 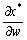 — симетрична, то
— симетрична, то
 (8.21)
(8.21)
тобто вплив зміни ціни на l-й ресурс на зміну попиту на j-й ресурс і зміна ціни на j-й ресурс на зміну попиту на l-й ресурс однакові.
Витрати j-го і l-го видів ресурсів є взаємозамінюваними (взаємодоповнюючими), якщо  тощо.
тощо.
Created/Updated: 25.05.2018