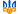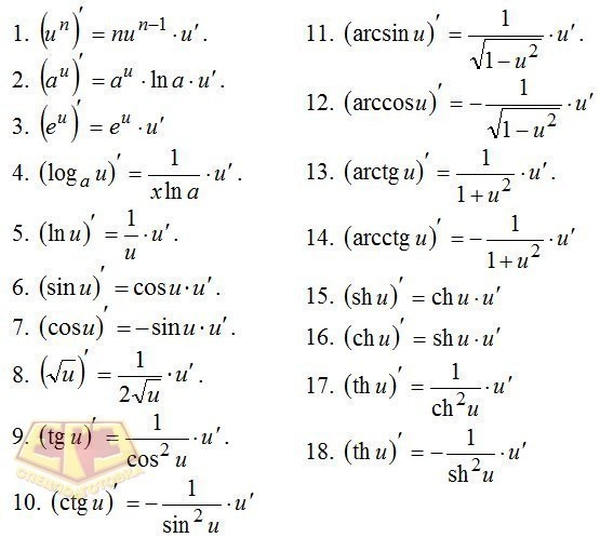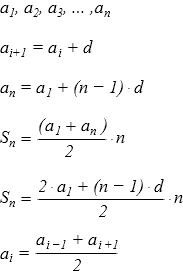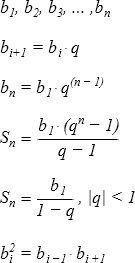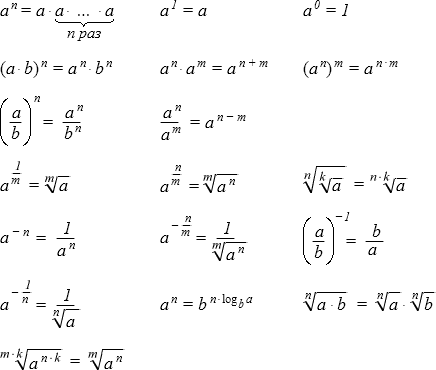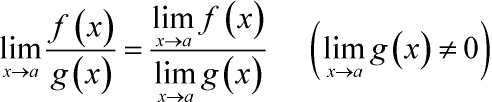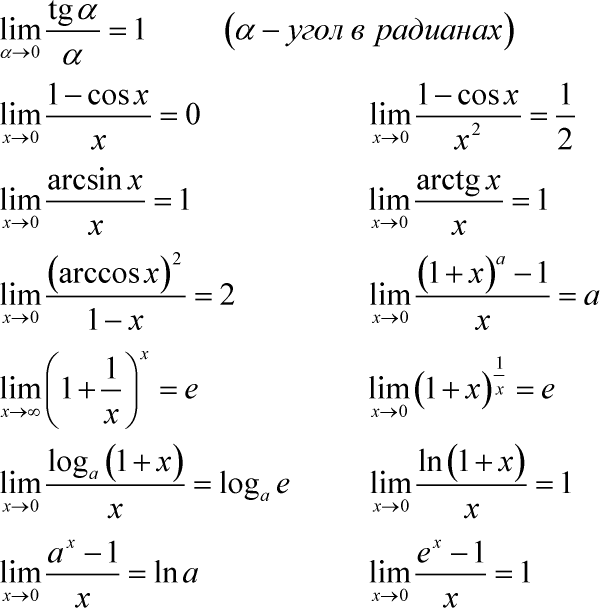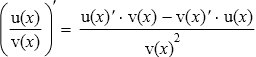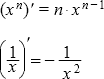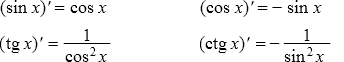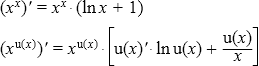Шпаргалки и Формулы
- Основные формулы ЕГЭ
- Математика для ЕГЭ
- Формулы для 11 класса
- Советская шпаргалка
- Элементарная математика
- Производные функций
- Таблица первообразных
- Тригонометрия и площади фигур
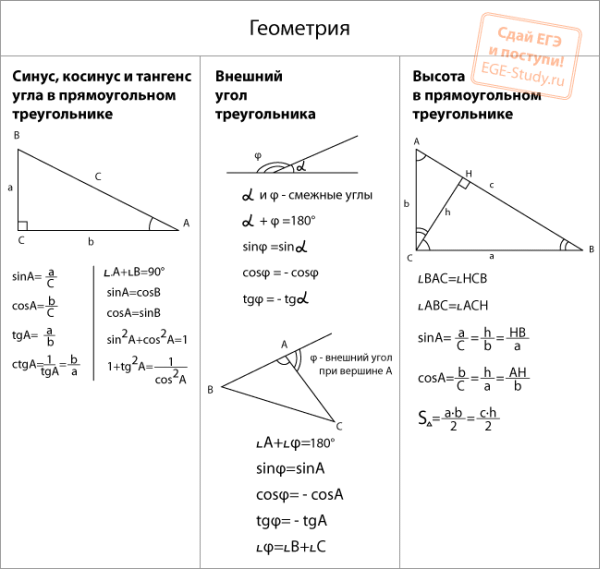
- Геометрия на ЕГЭ по математике
- Стереометрия
- Классическая стереометрия
- Алгебра
- Сокращенное умножение
- Тригонометрические формулы
- Прогрессии
- Степени и корни
- Логарифмы
- Пределы
- Таблица производных
- Решения уравнений Online
n Нажмите на изображение для просмотра в полном размере n
Таблица всех основных формул ЕГЭ
Шпаргалка по математике для ЕГЭ
Сборник формул для 11 класса
Старая добрая советская шпаргалка
Сборник формул по элементарной математике
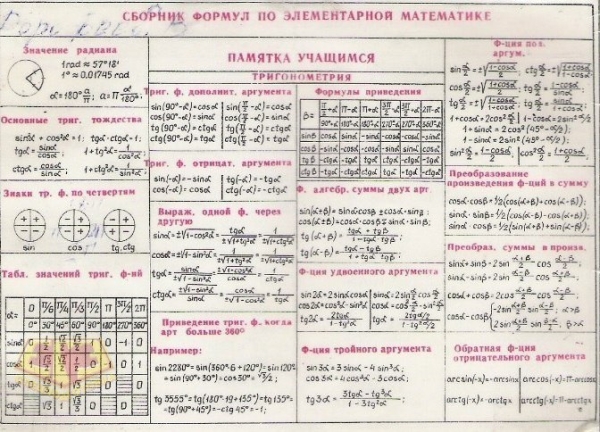
Формулы для производных функций
Таблица первообразных
Тригонометрия и площади фигур
Тригонометрический круг
Синус, косинус, тангенс…
Формулы тригонометрии
Геометрия. Площади фигур
Геометрия на ЕГЭ по математике. Треугольники, четырехугольники, окружности.
Высоты, медианы, биссектрисы
Параллелограмм, ромб, квадрат и их свойства
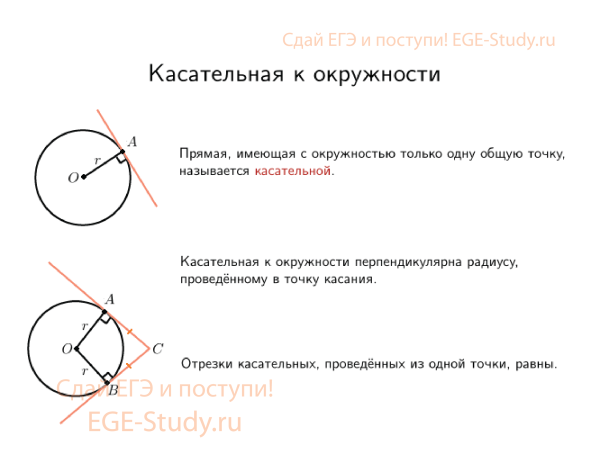
Касательная к окружности
Центральные и вписанные углы
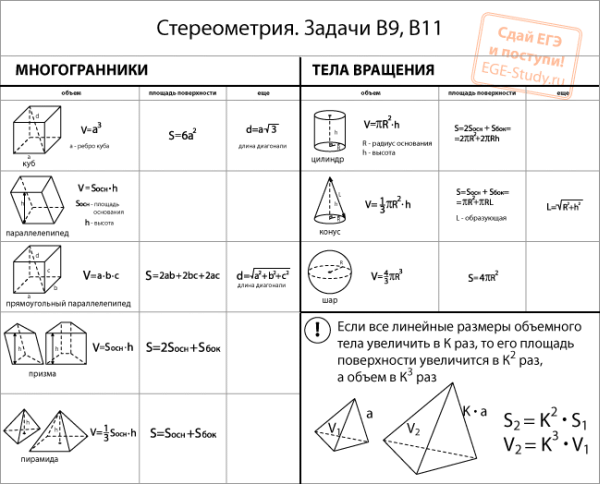
Стереометрия: формулы объема и площади поверхности.
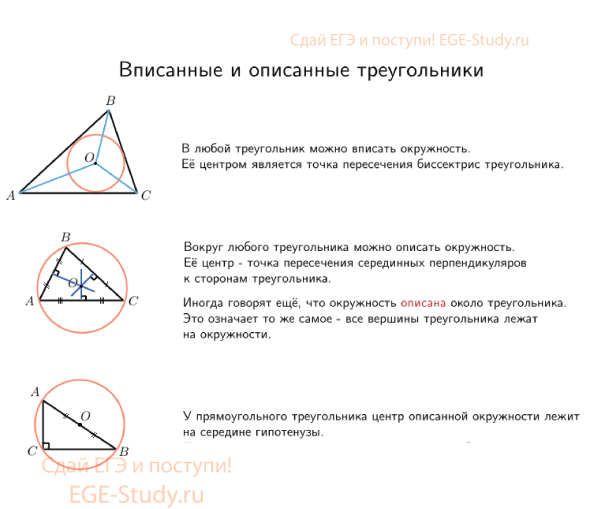
Вписанные и описанные треугольники
Вписанные и описанные четырехугольники
Стереометрия: Формулы объема и площади поверхности
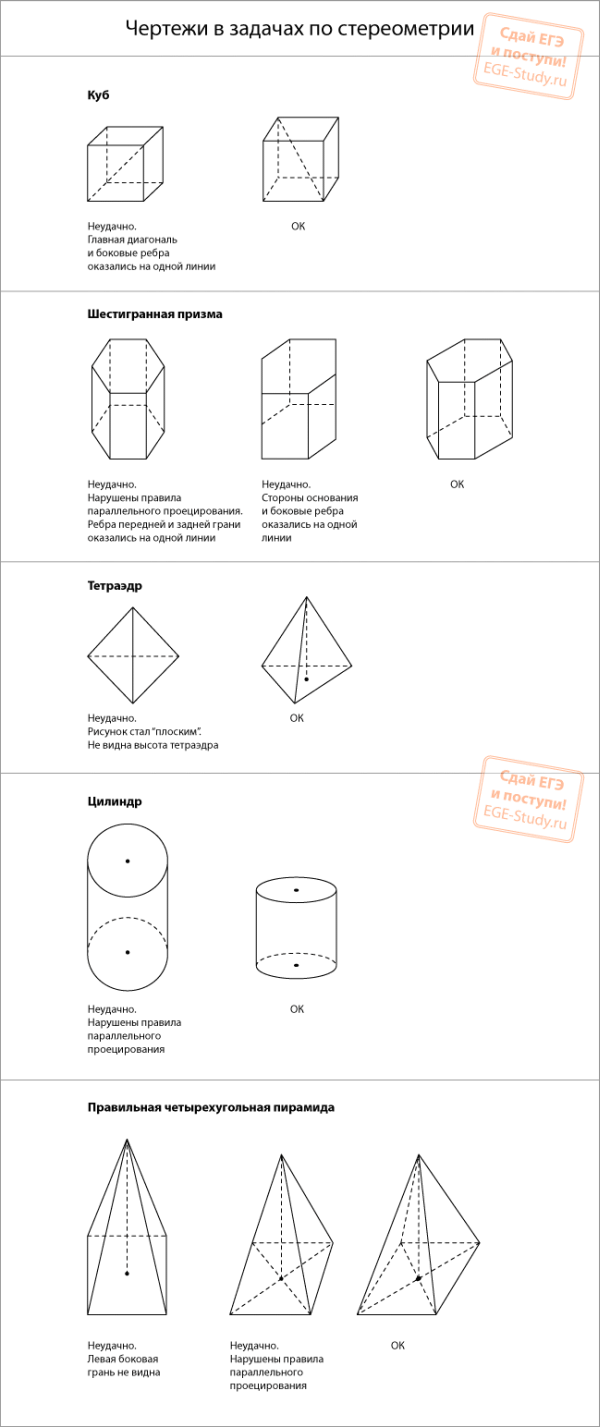
Чертежи в задачах по стереометрии
Классическая стереометрия и метод координат
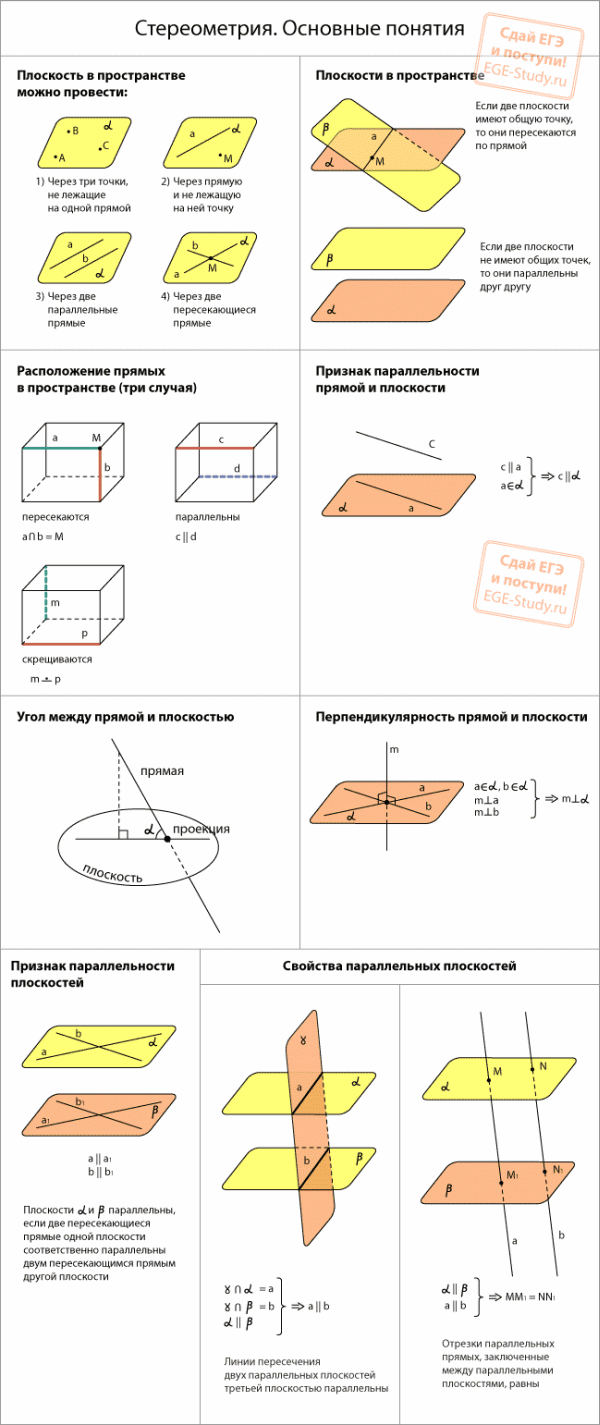
Основы стереометрии. Часть 1
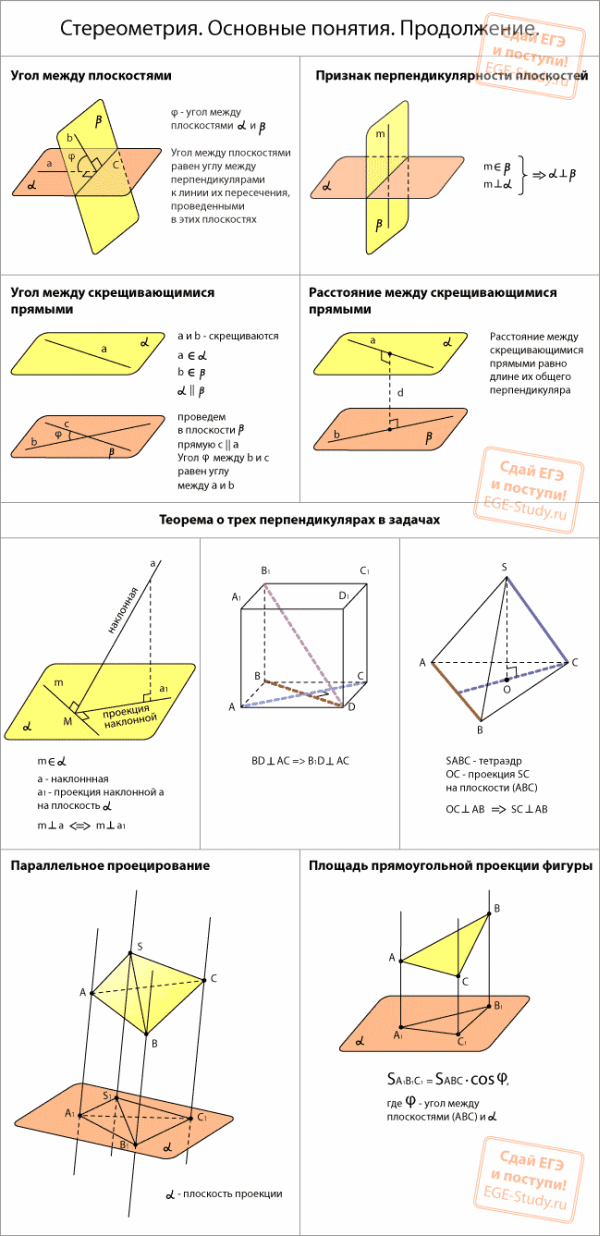
Основы стереометрии. Часть 2
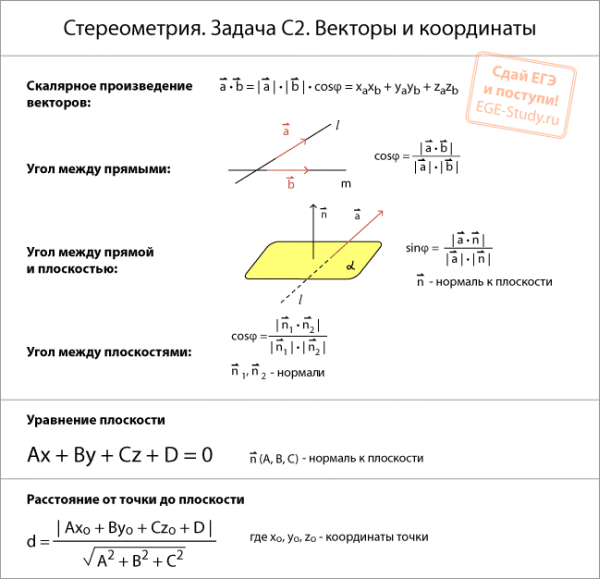
Стереометрия: Векторы и координаты
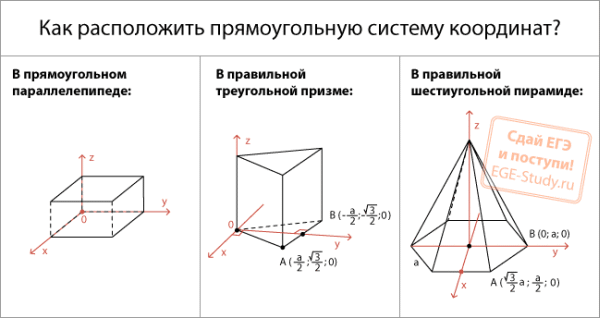
Как расположить прямоугольную систему координат
Алгебра
Таблица производных
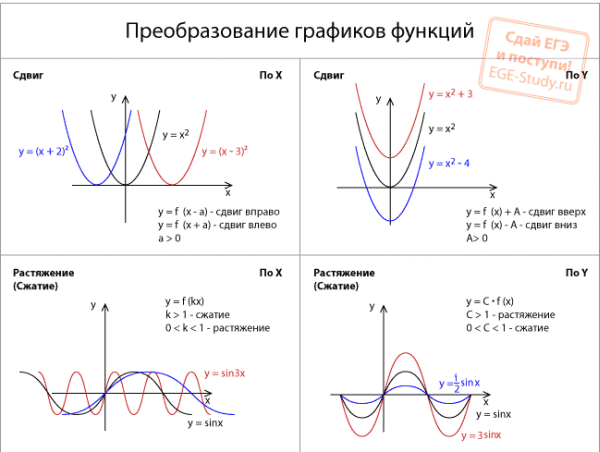
Преобразования графиков функций. Задача С5
Формулы сокращенного умножения
Квадрат суммы:
(a + b)2 = a2 + 2ab + b2
Квадрат разности:
(a - b)2 = a2 - 2ab + b2
Куб суммы:
(a + b)3 = a3 + 3a2b + 3b2a + b3
Куб разности:
(a - b)3 = a3 - 3a2b + 3b2a - b3
Формула Бинома-Ньютона:
(a + b)n = C0nan + C1nan-1b + ... + Cknan-kbk + Cnnbn, коэффициенты Ckn = n! / [k!(n ? k)!]
Сумма квадратов:
a2 + b2- не раскладывается
Разность квадратов:
a2 - b2 = (a - b)(a + b)
Сумма кубов:
a3 + b3 = (a + b)(a2 - ab + b2)
Разность кубов:
a3 - b3 = (a - b)(a2 + ab + b2)
(a + b)2 = a2 + 2ab + b2
Квадрат разности:
(a - b)2 = a2 - 2ab + b2
Куб суммы:
(a + b)3 = a3 + 3a2b + 3b2a + b3
Куб разности:
(a - b)3 = a3 - 3a2b + 3b2a - b3
Формула Бинома-Ньютона:
(a + b)n = C0nan + C1nan-1b + ... + Cknan-kbk + Cnnbn, коэффициенты Ckn = n! / [k!(n ? k)!]
Сумма квадратов:
a2 + b2- не раскладывается
Разность квадратов:
a2 - b2 = (a - b)(a + b)
Сумма кубов:
a3 + b3 = (a + b)(a2 - ab + b2)
Разность кубов:
a3 - b3 = (a - b)(a2 + ab + b2)
Тригонометрические формулы
Прогрессии
Степени и корни
Логарифмы
Пределы
Таблица производных
Created/Updated: 18.12.2021